香草和雪球是最近市场上比较火爆的金融衍生品,雪球和香草是奇异期权里障碍期权的一种,种类较多,分为大雪球、三园雪球、香草、季季红、多倍看涨等,其中三元雪球和香草为保本类,大雪球和多倍看涨是不保本的,对散户来说,如果不想了解过多的话,关注香草即可。这篇博客会详细介绍这几类金融衍生品,关注其交易规则和可能的底层金融资产。
Pytorch模型蒸馏Distillation
网络模型在部署时会通过剪枝蒸馏等方式加快推理速度,模型蒸馏大概可以分为通道蒸馏、特征蒸馏和目标蒸馏。这里需要特别强调的是,蒸馏的student网络学习的是teacher的泛化能力,而不是过拟合训练数据。这篇博客会以pytorch代码为基础,介绍常用的模型蒸馏方法。
UnrealCV部署使用指南
在深度学习中,数据仿真一直是重要的topic,Unreal(虚幻引擎)是Epic主导的渲染引擎,常被用于游戏、场景设计、渲染计算,也可以被用于深度学习中的数据仿真,其中有一些比较有名的基于Unreal开发的数据仿真平台,比如CARLA(http://carla.org/)、AirSim等优秀的仿真平台被用于自动驾驶、机器人自动控制等。这篇博客也是介绍一个这样的项目UnrealCV,简单介绍下unrealcv的部署和使用。实际上UnrealCV没有CARLA和AirSim强大(主要是没有运动模型和碰撞检测),所以简单介绍仅供参考。
Pytorch使用2d卷积来实现3d卷积
我们在深度学习模型转换和推理过程中常常会遇到算子不被工具链支持的情况,这时我们可以通过其它算子来等价实现我们想要的算子,比如3d卷积不被工具链支持,我们可以将其拆分成2d卷积,拆分之后我们需要进行权重字典的拆分。这篇博客贴一下pytorch的实现。
Vision Transformer
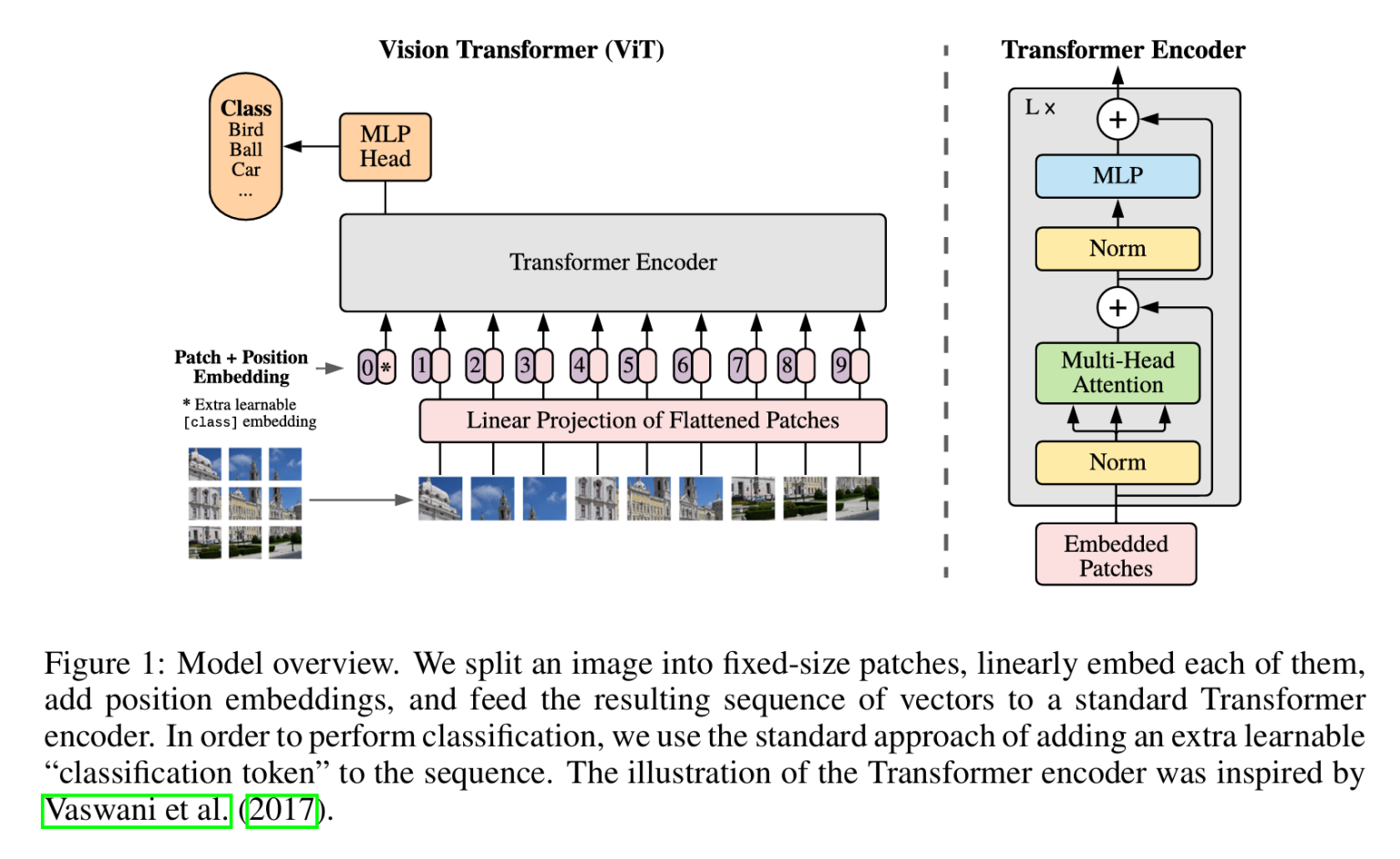
Transformer从NLP发展到视觉,开始改变视觉问题的处理方式,SwinTransformer和ViT都是典型的网络结构,典型的Transformer结构中大量使用Multi-Head Attention。ViT基于经典的Transformer模型,采用图像分块的方式将图像处理的问题转化为seq2seq的问题,这篇博客会从Attention开始,介绍到ViT。
神经网络训练量化(QAT)基本概念
QAT(Quantization Aware Training)量化感知训练是神经网络优化模型容量的重要方法,关系到模型精度和性能。pytorch对模型量化支持有三种方式:模型训练完毕后的动态量化、模型训练完毕后的静态量化、模型训练中开启量化QAT。这篇博客主要基于pytorh介绍QAT的基本概念。
使用OpCounter和flops-counter评估pytorch模型大小
在Pytorch中统计模型大小有一个非常好用的工具opcounters,opcounters用法也非常简单,这篇博客介绍opcounters用法。
几种3D传感器特点分析
目前的3D传感器可以大致划分成如下几种:双目传感器、单目传感器、三角雷达、线激光雷达、dTof、iTof、面阵 … 阅读更多
事件相机(三)事件相机特征提取
事件相机作为一种新型相机,其特征提取方法仍然有许多需要探索的地方,目前主流的事件相机特征提取算法都还是将事件信息二维化或者三维化,并没有很好利用事件相机数据量小的特点,也都把一些关键信息丢掉了,这篇博客主要介绍目前常用的事件相机的特征提取方法。用这些方法编码事件,有一些适合给传统算法使用,有一些适合使用CNN进行处理。
事件相机(二)事件相机应用
前面一篇博客介绍了事件相机的原理和种类,这一篇博客来介绍一下事件相机的具体应用场景,主要也是对 Event Camera Survey的总结梳理。目前学界研究比较多的是 SLAM、Motion Object Detection、Deblur、HDR、高帧率视频等方向。传统方法在SLAM上使用较多,提取事件特征非常繁琐耗费算力,NN方面在处理事件上有一些探索,但都还没完全成熟。目前主要的产品应用还是手机Deblur、插帧和HDR上(目前只有手机的出货量有机会压低Event Camera的成本)。
事件相机(一)事件相机原理
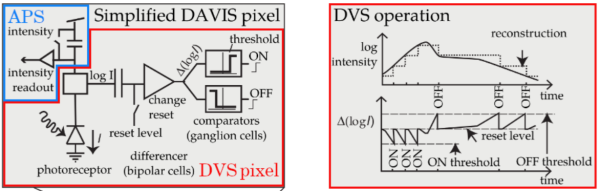
事件相机(Event Camera)目前分为如下几类:DVS、ATIS、DAVIS等,这类基于事件的相机与传统基于全帧输出的CIS相机不同,具有高帧率、高动态、低延时、低带宽的优点,同时也面临着噪声、Flicker、带宽变化等不利因素。这篇博客重点介绍事件相机产生事件的原理,和目前事件相机的分类。
CNN直接处理YUV图像
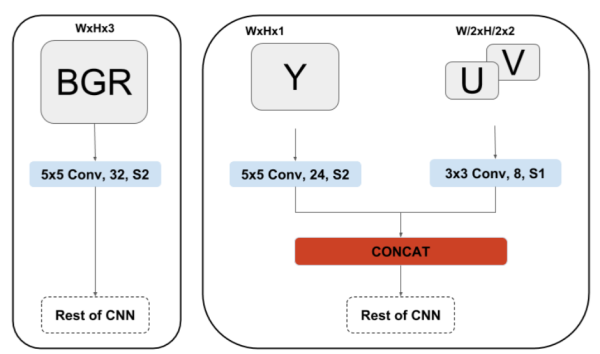
在ISP pipe中,最后输出的一般都是YUV图像,YUV420的数据量是RGB数据量的两倍,我们在送入CNN处理的时候处理RGB图像居多,如果CNN也可以直接输入YUV图像,那么前级需要的带宽就会减为输入RGB图的一半。
YUVMultiNet提供了一种实用的结构来处理YUV图像。这篇博客只会介绍处理YUV的这种结构,如果对MultiNet感兴趣可以移步原文:https://arxiv.org/pdf/1904.05673.pdf
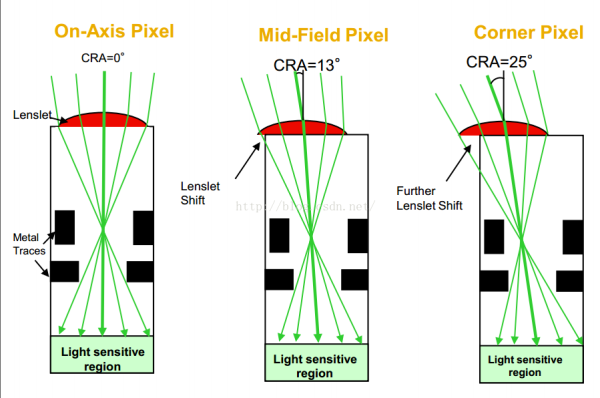
摄像头模组CRA参数
我们在摄像头模组规格书中和Sensor规格书中都会看到CRA这个光学参数。这里两个CRA的实际含义有所区别。镜头CRA的含义类似于FOV,Sensor CRA则关联传感器像素感光的量子效率。实际设计模组时这两个参数需要匹配。
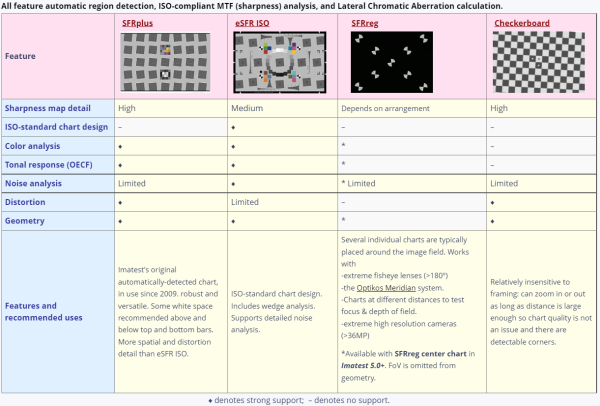
Matlab工具箱处理esfr_chart
ESFR chart是iso12233:2014中提供的一种chart,这种chart可以测sfr,也可以分析颜色误差、信噪比、Tone,我们除了使用imatest、dxo工具等专业影像分析工具外,我们也可以用Matlab的工具箱来处理esfr chart,测量成像系统的清晰度、信噪比等指标。
在Raw域控制饱和度的方法
我们在给图像乘以一定的gain的时候,如果各个通道乘的gain不同,会改变颜色和饱和度,所以我们在乘以gain … 阅读更多
Matlab最优化(一)线性规划
这系列博客开坑介绍Matlab最优化工具箱,处理如下最优化问题:线性规划、整数规划、非线性规划、二次规划、多目标规划、图与网络优化等。