博主之前刷过一遍《算法导论》(Introduction to Algorithms),但是看得多写得少,于是最近抽空动手写写下里面的算法。排序是经典问题了,于是决定将书中的排序算法一一使用C++实现。这篇博客一方面是对排序算法本身的总结(这个书上都有啦),另一方面是博主在使用C++实现算法时的一些体会,更多的是算法细节,希望有助于加深对算法的理解的。
排序算法总结
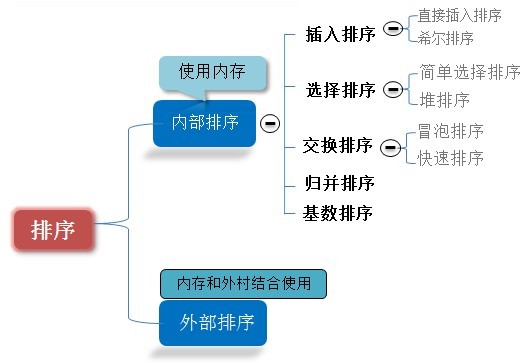
排序算法,介绍算法导论中的七种算法,它们的时间复杂度和空间复杂度如下表。插入排序代表了最坏的情况,归并排序,堆排序,快速排序基本都到达了使用内存排序算法的时间下界[mathjax]$latex n\lg (n)$,而后面三种排序,是使用了内存寻址的方式,实现了线性时间排序,桶排序是较为一般的方法,而基数排序和计数排序则需要被排序数字为整数。具体的实现推荐参考算法导论,这篇博客主要提供代码解释。
[table id=1 /]
[table id=2 /]
上面的gif摘自另一篇总结排序算法的博客。再简单介绍两种本博客不详细给出代码的算法。
鸡尾酒排序
鸡尾酒排序也叫作定向冒泡排序,与冒泡排序不同之处在于从低到高然后从高到低的比较每个元素,稍微提高了冒泡排序的性能。
希尔排序
希尔排序是插入排序的改进版本,但是希尔排序是不稳定的排序算法。改进之处在于将比较的全部元素分为几个区域来提升排序的性能。这样可以让一个元素一次性朝最终位置前进一大步,然后算法在取越来越小的步长进行排序,最后一步就是普通的插入排序。
插入排序
插入排序的核心就是维持一个循环不变式,在循环不变式内部的数组是已经排好序的,我们把后面的数组一个个的加进来。
#include <iostream>
#include <cstdio>
int insertionSort(int* a, int len){
// 核心是维持循环不变式
if (len < 2)
return 0;
for (int j = 1; j < len; ++j){
int i = j;
while (i >= 0){
if (a[i-1] > a[i]){
int tmp = a[i-1];
a[i-1] = a[i];
a[i] = tmp;
}
i--;
}
}
return 0;
}
int outputArray(int* a, int len){
for (int i = 0; i < len; ++i)
std::cout << a[i] << " ";
std::cout << std::endl;
return 0;
}
int heapSort(int *a, int length);
int mergeSort(int *a, int p, int r);
int quickSort(int *a, int p, int r);
int quickSortS(int *a, int p, int r);
int radixSort(int *a, int length);
int main(int argc, char *argv[]){
int a[13] = {12, 36, 34, 9, 35, 127, 55, 91, 82, 55, 64, 1000, 2};
insertionSort(a, 13);
//mergeSort(a, 0, 12);
//heapSort(a, 13);
//quickSortS(a, 0, 12);
//quickSort(a, 0, 12);
//radixSort(a, 13);
outputArray(a, 13);
system("pause");
return 0;
}
归并排序
归并排序采用了分解、解决、合并的分治策略。最重要的是合并步骤,也就是下面的merge函数,在merge中需要使用额外的内存,这是归并排序的不足。
#include <cstdio>
#include <iostream>
int merge(int *a, int p, int q, int r){
int nl = q - p + 1;
int nr = r - q;
int *L = new int[nl+1];
int *R = new int[nr+1];
for (int ii = 0; ii < nl; ++ii){
L[ii] = a[p+ii];
}
L[nl] = INT_MAX;
for (int ii = 0; ii < nr; ++ii){
R[ii] = a[q+ii+1];
}
R[nr] = INT_MAX;
int i = 0, j = 0;
for (int k = p; k <= r; ++k){
if (L[i] <= R[j]){
a[k] = L[i];
i++;
} else{
a[k] = R[j];
j++;
}
}
delete[] L, R;
return 0;
}
int mergeSort(int *a, int p, int r){
if (p < r){
int q = p + (r - p) / 2;
mergeSort(a, p, q);
mergeSort(a, q+1, r);
merge(a, p, q, r);
}
return 0;
}
堆排序
堆排序算法通过一个大(小)顶堆的性质来实现排序。大顶堆的性质是父亲比儿子们都要大,所以第一个元素总是最大的,在排序时不断将最大的元素提取出来,提取出来的元素就形成了排序后的数组。
此外,堆排序算法还可以形成一个优先队列,参考算法导论。
#include <cstdio>
#include <iostream>
inline int left(int i){
return 2 * i + 1;
}
inline int right(int i){
return 2 * i + 2;
}
inline int parent(int i){
return (i - 1) / 2;
}
int maxHeapify(int *a, int i, int heapsize){
int maxv = a[i];
int maxi = i;
if (left(i) < heapsize){
if (a[left(i)] > maxv){
maxv = a[left(i)];
maxi = left(i);
}
}
if (right(i) < heapsize){
if (a[right(i)] > maxv){
//maxv = a[right(i)];
maxi = right(i);
}
}
if (maxi != i){
int tmp = a[i];
a[i] = a[maxi];
a[maxi] = tmp;
maxHeapify(a, maxi, heapsize);
}
return 0;
}
int buildMaxHeap(int *a, int length){
for (int i = length/2-1; i >= 0; i--){
maxHeapify(a, i, length);
}
return 0;
}
int heapSort(int *a, int length){
buildMaxHeap(a, length);
for (int i = length - 1; i > 0; --i){
int tmp = a[i];
a[i] = a[0];
a[0] = tmp;
maxHeapify(a, 0, length);
}
return 0;
}
快速排序
快速排序也是通过分治策略来实现的排序,每次将一个元素排到正确位置。快速排序是原址排序,所以合并过程省略了,原址排序也是快速排序最大的优势。
此外,下面还贴出了针对相同元素的快速排序算法。相当于原快速排序是二指针问题,因为增加了一个区间,所以变成了三指针问题。
#include <cstdio>
#include <vector>
using namespace std;
int partition(int *a, int p, int r){
int x = a[r];
int i = p - 1, j = p;
for (int j = p; j < r; ++j){
if (a[j] <= x){
++i;
int tmp = a[j];
a[j] = a[i];
a[i] = tmp;
}
}
++i;
int tmp = a[i];
a[i] = a[r];
a[r] = tmp;
return i;
}
int quickSort(int *a, int p, int r){
if (p < r){
int q = partition(a, p, r);
quickSort(a, p, q-1);
quickSort(a, q+1, r);
}
return 0;
}
vector<int> partitionS(int *a, int p, int r){
vector<int> q;
int x = a[r];
int i = p, j = p, k = r;
while (j <= k){
if (a[j] > a[i]){
swap(a[j], a[k]);
k--;
} else if(a[j] < a[i]){
swap(a[j], a[i]);
i++;
j++;
} else{
j++;
}
}
q.push_back(i-1);
q.push_back(j);
return q;
}
int quickSortS(int *a, int p, int r){
if (p < r){
vector<int> q = partitionS(a, p, r);
quickSortS(a, p, q[0]);
quickSortS(a, q[1], r);
}
}
基数排序
基数排序虽然贴着线性时间的标签,但是常数项还是比较大的,就是通过对每个位进行一次稳定排序,来实现整体的排序。下面的代码中使用的是最低有效位的方式进行排序。
#include <cstdio>
#include <vector>
#include <algorithm>
using namespace std;
int radixSort(int *a, int len){
int base = 10;
int maxvalue = a[0];
for (int i = 1; i < len; ++i){
if (a[i] > maxvalue){
maxvalue = a[i];
}
}
vector<vector<int>> buckets(base);
for (int i = 1; i <= maxvalue; i = i*base){
for (int j = 0; j < len; j++){
buckets[(a[j] / i) % base].push_back(a[j]);
}
int k = 0;
for (int j = 0; j < base; j++){
for (auto num : buckets[j]){
a[k++] = num;
}
buckets[j].clear();
}
}
return 0;
}
计数排序&桶排序
这个就不多讲了,计数排序直接将数组下标作为地址,而计数排序就可以看做桶大小为1的桶排序。