LeetCode_011: Container With Most Water

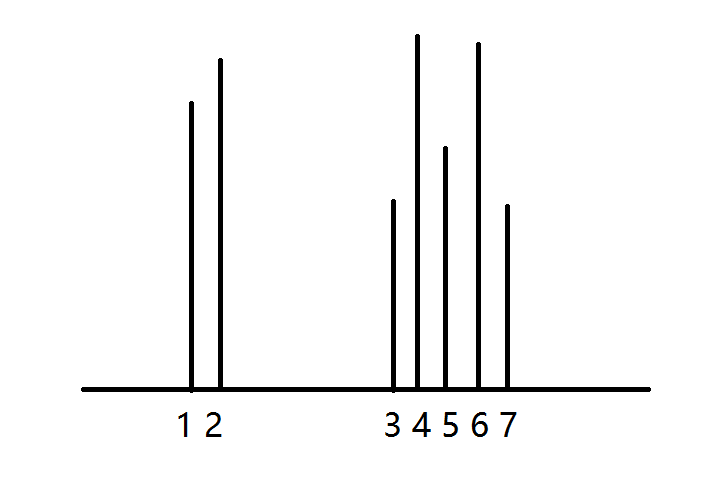
        这道题的重点是对双指针过程的分析，典型的双指针类型题目，博主的代码速度为16ms，战胜90%的答题者，思路比较一般，不过还是分享一下。

题目

Given n non-negative integers a₁, a₂, …, a_n, where each represents a point at coordinate (i, a_i). n vertical lines are drawn such that the two endpoints of line i is at (i, a_i) and (i, 0). Find two lines, which together with x-axis forms a container, such that the container contains the most water.

Note: You may not slant the container and n is at least 2.

分析

分析过程如下，现在有两个指针从左右两端向中间移动，那么盛水的体积等于左右指针指向的最小高度乘以宽度。[mathjax]

如果$latex H(left) < H(right)$，那么盛水的体积取决于左边的指针，那么现在开始移动左边的指针。

在移动过程中，更新最小高度，如果发现之后的高度小于之前的高度，那么直接跳过（因为向中间移动的时候宽度肯定变小了，如果高度再变小，那么容积肯定变小），如果发现高度大于之前的高度，那么判断容积。最后返回最大容积即可。 

代码

class Solution {
public:
	int maxArea(vector<int>& height) {
		int i = 0, j = height.size() - 1;
		int area = min(height[i], height[j]) * (j - i);
		int len = j;
		while (i != j){
		    len--;
			if (height[i] < height[j]){
				i++;
				if (height[i] <= height[i - 1]){
					continue;
				} else{
					area = max(area, min(height[i], height[j]) * len);
				}
			} else{
				j--;
				if (height[j] <= height[j + 1]){
					continue;
				} else{
					area = max(area, min(height[i], height[j]) * len);
				}
			}
		}
		return area;
	}
};