最近总是Rank到很难的题目,这次遇到了LeetCode中通过率最低的题目。这道题目是一个图相关的问题,同时牵扯到很多坑,很多细节,即使思路正确稍不注意内存超出,时间超出都是常事儿,自己做出来还是需要废一番功夫的。博主写了BFS算法的大概就放弃了,后面翻了几份代码,找了个最简洁的 ,这里也只能讲解一下别人的代码了。
题目
Given two words (beginWord and endWord), and a dictionary’s word list, find all shortest transformation sequence(s) from beginWord toendWord, such that:
- Only one letter can be changed at a time
- Each transformed word must exist in the word list. Note that beginWord is not a transformed word.
For example,
Given:
beginWord ="hit"
endWord ="cog"
wordList =["hot","dot","dog","lot","log","cog"]Return
[ [“hit”,”hot”,”dot”,”dog”,”cog”], [“hit”,”hot”,”lot”,”log”,”cog”] ]
Note:
- Return an empty list if there is no such transformation sequence.
- All words have the same length.
- All words contain only lowercase alphabetic characters.
- You may assume no duplicates in the word list.
- You may assume beginWord and endWord are non-empty and are not the same.
UPDATE (2017/1/20):
The wordList parameter had been changed to a list of strings (instead of a set of strings). Please reload the code definition to get the latest changes.
分析
这里直接看代码吧,基本思路就是转化为一个图搜索问题,下面只介绍几个坑:
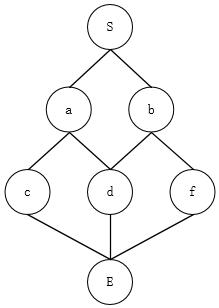
1. 因为要寻找所有的最短路径,设置visited、finished的时候,要在一层都处理完之后再设置,如上图,b和a同时可以到达d点,使用传统dfs就会少一条路径。
2. 使用邻接链表来处理连接点,这个连接是单向的,这是为了避免后面DFS找到更远的路径
3. 通过BFS来记录连接,后面通过DFS来恢复路径
其它地方都在代码里面写了注释
代码
注释版本,后面还有未带注释的版本,看着简洁舒服很多
class Solution {
/*
Idea :
1. use two-end bfs to iteratively find the shortest path
2. use a map of [nextNode, curNodeList] to record all possible paths to the nextNode for the purpose of backtracing
3. use a boolean to represent the end of bfs, a boolean to represent the swap of head and tail
4. use dfs to recursivlely backtrace
Caution and more ideas : see comments
*/
public:
vector<vector<string>> findLadders(string beginWord, string endWord, vector<string>& wordList){
unordered_set<string> s;
for (auto item : wordList){
s.insert(item);
}
if (s.find(endWord) == s.end()){
return{};
}
unordered_map<string, unordered_set<string>> backtrace;
unordered_set<string> head({ beginWord }), tail({endWord});
bool reverse = false, finish = false;
s.erase(beginWord); s.erase(endWord);
while (!head.empty() && !tail.empty() && !finish){
// two-end bfs: swap head and tail to reach balence of two sets
// for optimized performance
if (head.size() > tail.size()){
reverse = !reverse;
swap(head, tail);
}
// temp will contain neighbors of the current level nodes, so this is bfs
unordered_set<string> temp;
for (auto item : head){
for (int l = 0; l < item.size(); ++l){ // 对单词中每个字母进行26个字母的替换
string ori = item;
// O(26 * size of item)
for (char c = 'a'; c <= 'z'; ++c){
item[l] = c;
if (tail.find(item) != tail.end()){ // 查寻等于尾部节点
if (!reverse){
backtrace[item].insert(ori); // backtrace 是用来记录路径的邻接链表 map<string,vec<string>>, string中的每个元素都与vec<string>中的元素相差一个字符,这个连接是带有方向的,保证在dfs时不出现更长的字符串
} else{
backtrace[ori].insert(item);
}
finish = true;
} else if (s.find(item) != s.end()){ // 在没有查找到尾部节点的情况下,在词典中查找
temp.insert(item); // 搜索新起点
if (!reverse){
backtrace[item].insert(ori); // backtrace被用来记录路径,方式为邻接链表
} else{
backtrace[ori].insert(item);
}
}
}
item = ori; // 与前面ori=item相呼应,这里进行的是item的还原
}
}
// only delete items after we finish iterating the current level
// if we delete while iterating, it is possible that we delete a
// node whice has two sources to reach it
for (auto item : temp){ // because all temp are visited,这里注意,不立即标识visitied,而在访问完一层之后标识visited,就是为了在bfs时不会引起一些路径的丢失,finish 也是一轮之后才生效,这样才能找到所有最短的结果
s.erase(item);
}
head = temp;
}
vector<vector<string>> ret;
vector<string> temp({endWord});
backtrack(ret, backtrace, temp, endWord, beginWord); // recover paths
return ret;
}
private:
void backtrack(vector<vector<string>> &ret,
unordered_map<string, unordered_set<string>>& backtrace,
vector<string>& temp,
string endWord,
string beginWord){
if (endWord == beginWord){ // 剪枝条件
vector<string> rev = temp;
reverse(rev.begin(), rev.end());
ret.push_back(rev);
return;
}
for (auto item : backtrace[endWord]){ // 在最后到达endWord的所有结果进行DFS回溯
temp.push_back(item);
backtrack(ret, backtrace, temp, item, beginWord); // endWord是深度优先搜索的变化量
temp.pop_back();
}
return;
}
};
不带注释版本的代码:
class Solution {
public:
vector<vector<string>> findLadders(string beginWord, string endWord, vector<string>& wordList){
unordered_set<string> s;
for (auto item : wordList){
s.insert(item);
}
if (s.find(endWord) == s.end()){
return{};
}
unordered_map<string, unordered_set<string>> backtrace;
unordered_set<string> head({ beginWord }), tail({endWord});
bool reverse = false, finish = false;
s.erase(beginWord); s.erase(endWord);
while (!head.empty() && !tail.empty() && !finish){
if (head.size() > tail.size()){
reverse = !reverse;
swap(head, tail);
}
unordered_set<string> temp;
for (auto item : head){
for (int l = 0; l < item.size(); ++l){
string ori = item;
for (char c = 'a'; c <= 'z'; ++c){
item[l] = c;
if (tail.find(item) != tail.end()){
if (!reverse){
backtrace[item].insert(ori);
} else{
backtrace[ori].insert(item);
}
finish = true;
} else if (s.find(item) != s.end()){
temp.insert(item);
if (!reverse){
backtrace[item].insert(ori);
} else{
backtrace[ori].insert(item);
}
}
}
item = ori;
}
for (auto item : temp){
s.erase(item);
}
head = temp;
}
vector<vector<string>> ret;
vector<string> temp({endWord});
backtrack(ret, backtrace, temp, endWord, beginWord);
return ret;
}
private:
void backtrack(vector<vector<string>> &ret,
unordered_map<string, unordered_set<string>>& backtrace,
vector<string>& temp,
string endWord,
string beginWord){
if (endWord == beginWord){
vector<string> rev = temp;
reverse(rev.begin(), rev.end());
ret.push_back(rev);
return;
}
for (auto item : backtrace[endWord]){
temp.push_back(item);
backtrack(ret, backtrace, temp, item, beginWord);
temp.pop_back();
}
return;
}
};