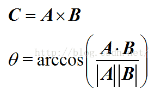Matlab计算旋转矩阵有两种方法,一种是通过欧拉角,计算yaw,pitch和row轴的旋转角。这里要介绍的是另一种是直接绕一个向量旋转theta角的方法,就是Rodrigues变换,其中的向量就是旋转向量,其得到的矩阵就是旋转矩阵,这个矩阵和欧拉角的方法计算出来是一样的。
而我们常常将旋转和平移组合在一个3*4的矩阵中,使得物体三维坐标乘以该矩阵,直接得到旋转平移变换之后的坐标。此时就需要将旋转向量转化为一个3×3的旋转矩阵,这就是罗德里格斯(Rodrigues)变换。
一、Rodrigues变换的数学原理
如题,旋转有两种理解,一种是绕坐标轴依次旋转,另一种是绕任意轴一次直接旋转一个角度得到。将向量B看做是A绕着轴C转过角度theta得到,则:
同时,我们还要求norm(C)=theta,于是,旋转向量方向与C相同,向量的模大小是弧度制的角度,我们就可以很轻松的求出两个向量的旋转向量和旋转矩阵了。
% 求向量A和向量B的旋转矩阵 clear A = [-0.9772 0.0953 -0.1896]'; B = [-0.9937 0.0999 0.0501]'; C = cross(B, A); theta = acos((A'*B) / ( norm(A)*norm(B) )); Rv = C / norm(C) * theta; R = rodrigues(Rv);
二、Rodrigues变换的实现
在OpenCV和Matlab中都用实现Rodrigues变换:
OpenCV中Calib模块有实现该函数,查看OpenCV文档中的解释,和一篇博客。
正反变换都是同一个函数,输入1*3或3*1,输出3*3,或者输入3*3,输出1*3,第三个参数还可以输出3*9的雅可比矩阵
cv::Mat om(3, 1, CV_32FC1);
om.ptr<float>(0)[0] = p[0];
om.ptr<float>(1)[0] = p[1];
om.ptr<float>(2)[0] = p[2];
cv::Mat R(3, 3, CV_32FC1);
cv::Rodrigues(om, R);
for (int i = 0; i < 3; ++i){
for (int j = 0; j < 3; ++j){
mat[i][j] = R.ptr<float>(i)[j];
}
}
一个工具箱中,Matlab实现rodrigues变换的函数,与上面opencv使用是类似的
function [out,dout]=rodrigues(in)
% RODRIGUES Transform rotation matrix into rotation vector and viceversa.
%
% Sintax: [OUT]=RODRIGUES(IN)
% If IN is a 3x3 rotation matrix then OUT is the
% corresponding 3x1 rotation vector
% if IN is a rotation 3-vector then OUT is the
% corresponding 3x3 rotation matrix
%
%%
%% Copyright (c) March 1993 -- Pietro Perona
%% California Institute of Technology
%%
%% ALL CHECKED BY JEAN-YVES BOUGUET, October 1995.
%% FOR ALL JACOBIAN MATRICES !!! LOOK AT THE TEST AT THE END !!
%% BUG when norm(om)=pi fixed -- April 6th, 1997;
%% Jean-Yves Bouguet
%% Add projection of the 3x3 matrix onto the set of special ortogonal matrices SO(3) by SVD -- February 7th, 2003;
%% Jean-Yves Bouguet
% BUG FOR THE CASE norm(om)=pi fixed by Mike Burl on Feb 27, 2007
[m,n] = size(in);
%bigeps = 10e+4*eps;
bigeps = 10e+20*eps;
if ((m==1) & (n==3)) | ((m==3) & (n==1)) %% it is a rotation vector
theta = norm(in);
if theta < eps
R = eye(3);
%if nargout > 1,
dRdin = [0 0 0;
0 0 1;
0 -1 0;
0 0 -1;
0 0 0;
1 0 0;
0 1 0;
-1 0 0;
0 0 0];
%end;
else
if n==length(in) in=in'; end; %% make it a column vec. if necess.
%m3 = [in,theta]
dm3din = [eye(3);in'/theta];
omega = in/theta;
%m2 = [omega;theta]
dm2dm3 = [eye(3)/theta -in/theta^2; zeros(1,3) 1];
alpha = cos(theta);
beta = sin(theta);
gamma = 1-cos(theta);
omegav=[[0 -omega(3) omega(2)];[omega(3) 0 -omega(1)];[-omega(2) omega(1) 0 ]];
A = omega*omega';
%m1 = [alpha;beta;gamma;omegav;A];
dm1dm2 = zeros(21,4);
dm1dm2(1,4) = -sin(theta);
dm1dm2(2,4) = cos(theta);
dm1dm2(3,4) = sin(theta);
dm1dm2(4:12,1:3) = [0 0 0 0 0 1 0 -1 0;
0 0 -1 0 0 0 1 0 0;
0 1 0 -1 0 0 0 0 0]';
w1 = omega(1);
w2 = omega(2);
w3 = omega(3);
dm1dm2(13:21,1) = [2*w1;w2;w3;w2;0;0;w3;0;0];
dm1dm2(13: 21,2) = [0;w1;0;w1;2*w2;w3;0;w3;0];
dm1dm2(13:21,3) = [0;0;w1;0;0;w2;w1;w2;2*w3];
R = eye(3)*alpha + omegav*beta + A*gamma;
dRdm1 = zeros(9,21);
dRdm1([1 5 9],1) = ones(3,1);
dRdm1(:,2) = omegav(:);
dRdm1(:,4:12) = beta*eye(9);
dRdm1(:,3) = A(:);
dRdm1(:,13:21) = gamma*eye(9);
dRdin = dRdm1 * dm1dm2 * dm2dm3 * dm3din;
end;
out = R;
dout = dRdin;
%% it is prob. a rot matr.
elseif ((m==n) & (m==3) & (norm(in' * in - eye(3)) < bigeps)...
& (abs(det(in)-1) < bigeps))
R = in;
% project the rotation matrix to SO(3);
[U,S,V] = svd(R);
R = U*V';
tr = (trace(R)-1)/2;
dtrdR = [1 0 0 0 1 0 0 0 1]/2;
theta = real(acos(tr));
if sin(theta) >= 1e-4,
dthetadtr = -1/sqrt(1-tr^2);
dthetadR = dthetadtr * dtrdR;
% var1 = [vth;theta];
vth = 1/(2*sin(theta));
dvthdtheta = -vth*cos(theta)/sin(theta);
dvar1dtheta = [dvthdtheta;1];
dvar1dR = dvar1dtheta * dthetadR;
om1 = [R(3,2)-R(2,3), R(1,3)-R(3,1), R(2,1)-R(1,2)]';
dom1dR = [0 0 0 0 0 1 0 -1 0;
0 0 -1 0 0 0 1 0 0;
0 1 0 -1 0 0 0 0 0];
% var = [om1;vth;theta];
dvardR = [dom1dR;dvar1dR];
% var2 = [om;theta];
om = vth*om1;
domdvar = [vth*eye(3) om1 zeros(3,1)];
dthetadvar = [0 0 0 0 1];
dvar2dvar = [domdvar;dthetadvar];
out = om*theta;
domegadvar2 = [theta*eye(3) om];
dout = domegadvar2 * dvar2dvar * dvardR;
else
if tr > 0; % case norm(om)=0;
out = [0 0 0]';
dout = [0 0 0 0 0 1/2 0 -1/2 0;
0 0 -1/2 0 0 0 1/2 0 0;
0 1/2 0 -1/2 0 0 0 0 0];
else
% case norm(om)=pi;
if(0)
%% fixed April 6th by Bouguet -- not working in all cases!
out = theta * (sqrt((diag(R)+1)/2).*[1;2*(R(1,2:3)>=0)'-1]);
%keyboard;
else
% Solution by Mike Burl on Feb 27, 2007
% This is a better way to determine the signs of the
% entries of the rotation vector using a hash table on all
% the combinations of signs of a pairs of products (in the
% rotation matrix)
% Define hashvec and Smat
hashvec = [0; -1; -3; -9; 9; 3; 1; 13; 5; -7; -11];
Smat = [1,1,1; 1,0,-1; 0,1,-1; 1,-1,0; 1,1,0; 0,1,1; 1,0,1; 1,1,1; 1,1,-1;
1,-1,-1; 1,-1,1];
M = (R+eye(3,3))/2;
uabs = sqrt(M(1,1));
vabs = sqrt(M(2,2));
wabs = sqrt(M(3,3));
mvec = ([M(1,2), M(2,3), M(1,3)] + [M(2,1), M(3,2), M(3,1)])/2;
syn = ((mvec > eps) - (mvec < -eps)); % robust sign() function
hash = syn * [9; 3; 1];
idx = find(hash == hashvec);
svec = Smat(idx,:)';
out = theta * [uabs; vabs; wabs] .* svec;
end;
if nargout > 1,
fprintf(1,'WARNING!!!! Jacobian domdR undefined!!!\n');
dout = NaN*ones(3,9);
end;
end;
end;
else
error('Neither a rotation matrix nor a rotation vector were provided');
end;
return;
%% test of the Jacobians:
%% TEST OF dRdom:
om = randn(3,1);
dom = randn(3,1)/1000000;
[R1,dR1] = rodrigues(om);
R2 = rodrigues(om+dom);
R2a = R1 + reshape(dR1 * dom,3,3);
gain = norm(R2 - R1)/norm(R2 - R2a)
%% TEST OF dOmdR:
om = randn(3,1);
R = rodrigues(om);
dom = randn(3,1)/10000;
dR = rodrigues(om+dom) - R;
[omc,domdR] = rodrigues(R);
[om2] = rodrigues(R+dR);
om_app = omc + domdR*dR(:);
gain = norm(om2 - omc)/norm(om2 - om_app)
%% OTHER BUG: (FIXED NOW!!!)
omu = randn(3,1);
omu = omu/norm(omu)
om = pi*omu;
[R,dR]= rodrigues(om);
[om2] = rodrigues(R);
[om om2]
%% NORMAL OPERATION
om = randn(3,1);
[R,dR]= rodrigues(om);
[om2] = rodrigues(R);
[om om2]
%% Test: norm(om) = pi
u = randn(3,1);
u = u / sqrt(sum(u.^2));
om = pi*u;
R = rodrigues(om);
R2 = rodrigues(rodrigues(R));
norm(R - R2)
%% Another test case where norm(om)=pi from Chen Feng (June 27th, 2014)
R = [-0.950146567583153 -6.41765854280073e-05 0.311803617668748; ...
-6.41765854277654e-05 -0.999999917385145 -0.000401386434914383; ...
0.311803617668748 -0.000401386434914345 0.950146484968298];
om = rodrigues(R)
norm(om) - pi
%% Another test case where norm(om)=pi from 浣欐垚涔�(July 1st, 2014)
R = [-0.999920129411407 -6.68593208347372e-05 -0.0126384464118876; ...
9.53007036072085e-05 -0.999997464662094 -0.00224979713751896; ...
-0.0126382639492467 -0.00225082189773293 0.999917600647740];
om = rodrigues(R)
norm(om) - pi
上面的matlab函数来自加州理工的张正友标定工具箱。