各种不同的卷积滤波核有不同的频率响应特性,我们以bicubic插值kernel为例,用Matlab绘制出频谱图,可以看出卷积后哪些频率成分会被加强,哪些频率成分会被减弱。
首先分享一个介绍图像傅立叶变换的资料:https://www.cs.unm.edu/~brayer/vision/fourier.html
我们以bicubic插值kernel为例,先定义一个二维卷积核,d在0-1之间,表示采样相位,a在 -1 到 0 之间,表示采样kernel的形状:
function k = bicubic_kernel(d, a) k1 = zeros(4,1); k1(1) = bicubic_wt(d-2, a); k1(2) = bicubic_wt(d-1, a); k1(3) = bicubic_wt(d, a); k1(4) = bicubic_wt(d+1, a); k = k1*k1'; end function r = bicubic_wt(d, a) d = abs(d); d2 = d*d; d3 = d2*d; r1 = (a+2)*d3 - (a+3)*d2 + 1; r2 = a * d3 - 5*a*d2 + 8*a*d - 4*a; r = (d<=1) * r1 + (d>1&&d<=2)*r2; end
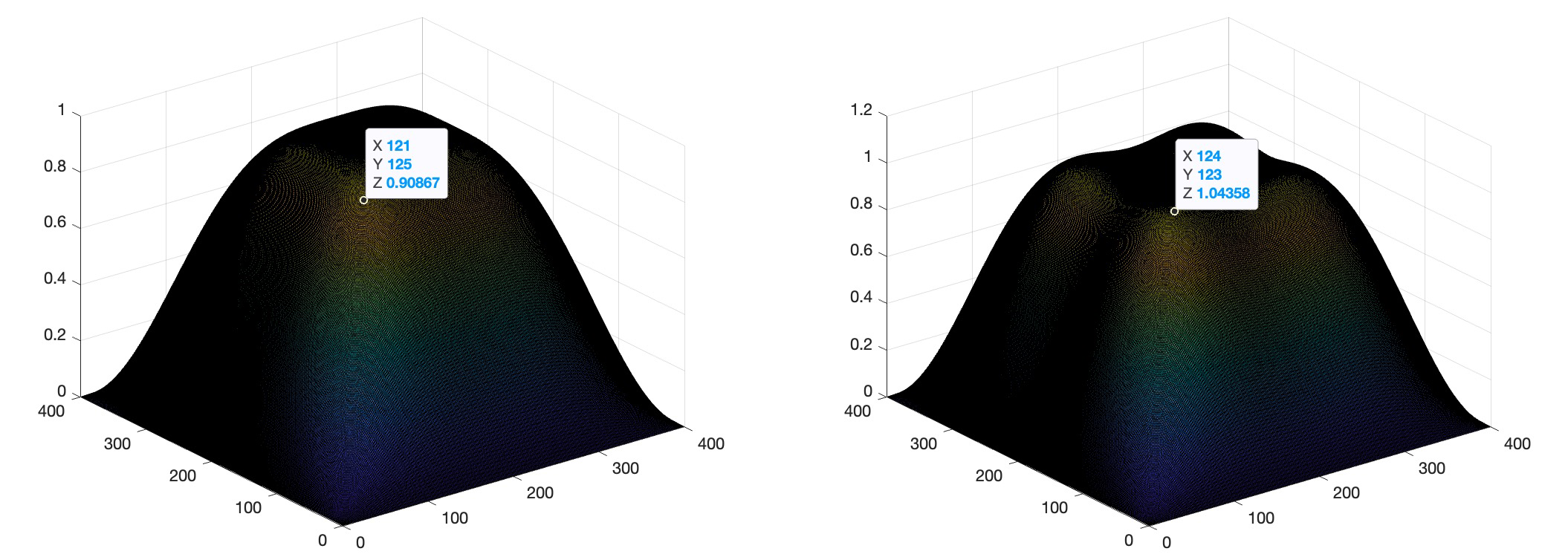
接下来我们做一个实验,首先,看一个周期纹理的频谱,然后,看下两个bicubic kernel的频谱响应,kernel fft之后大于1的区域,会因为卷积加强对影频率成分,反应在kernel fft之后幅度谱上,就是大于1的值,就是代码中打印出的sp点。
I = zeros(400, 400);
%I(1:4:end,:) = 1;
I(1:4:end,1:4:end) = 1;
Y = fft2(I,1600,1600);
figure('Color','White','Position',[0,0,1150,450])
subplot(121),imshow(I);
subplot(122),imagesc(abs(fftshift(Y)));
k1 = bicubic_kernel(0.5, -0.5);
k2 = bicubic_kernel(0.5, -0.75);
f1 = fft2(k1, 400, 400);
f2 = fft2(k2, 400, 400);
m1 = abs(fftshift(f1));
m2 = abs(fftshift(f2));
figure('Color','White')
subplot(121),imagesc(k1);
subplot(122),imagesc(abs(fftshift(f1)));
figure('Color','White')
subplot(121),imagesc(k2);
subplot(122),imagesc(abs(fftshift(f2)));
figure('Color', 'White'), surf(abs(fftshift(f1)))
figure('Color', 'White'), surf(abs(fftshift(f2)))
sp = 200-70;
m1(sp, sp)
m2(sp, sp)
画出来是这样: