经典的题目,最开始没想到这种解法,只想着用优先队列去解了,看了下答案,大概有两种解法,一种是DP,另一种是维护一个栈,这种解法应该是见过最好的了。惯例,贡献高质量解法。
题目
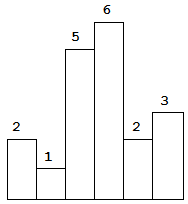
Given n non-negative integers representing the histogram’s bar height where the width of each bar is 1, find the area of largest rectangle in the histogram.
Above is a histogram where width of each bar is 1, given height =
[2,1,5,6,2,3].
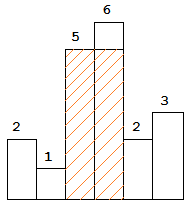
The largest rectangle is shown in the shaded area, which has area =
10unit.For example,
Given heights =[2,1,5,6,2,3],
return10.
分析
这里主要是维护一个栈,这个栈存储的是数组的小标。并且栈中元素从底向上,高度是依次递增的。
也就是说,再往后面搜索时,高峰会被磨平,栈中记录的,都是高于当前区间有效值的低谷值。如在搜索21时,取决于1,搜索到215时,就自动试做115,第一个1省略了,栈记录最新的低谷。
算法遍历原直方图数组每个bar,如果栈顶元素比当前bar的元素高或相等,那么就一直出栈,并计算元素值。关于算法的理解,参见这篇博客的解释(虽然代码不同,但大致意思相同,我把它摘录在下面)。
For example,
Given height =[2,1,5,6,2,3],
return10.首先想到一种最直观的方法:把平面看做大矩阵,条形看做1,非条形看做0,寻找最大全1矩阵。
思路上是正确的,可以用DP来做,不过会超时。
网上看到一种借助栈的做法,代码很漂亮,但是解释都非常模糊,我看懂之后,决定仔细描述思路如下:
1、如果已知height数组是升序的,应该怎么做?
比如1,2,5,7,8
那么就是(1*5) vs. (2*4) vs. (5*3) vs. (7*2) vs. (8*1)
也就是max(height[i]*(size-i))
2、使用栈的目的就是构造这样的升序序列,按照以上方法求解。
但是height本身不一定是升序的,应该怎样构建栈?
比如2,1,5,6,2,3
(1)2进栈。s={2}, result = 0
(2)1比2小,不满足升序条件,因此将2弹出,并记录当前结果为2*1=2。
将2替换为1重新进栈。s={1}, result = 2
(3)5比1大,满足升序条件,进栈。s={1,5},result = 2
(4)6比5大,满足升序条件,进栈。s={1,5,6},result = 2
(5)2比6小,不满足升序条件,因此将6弹出,并记录当前结果为6*1=6。s={1,5},result = 6
2比5小,不满足升序条件,因此将5弹出,并记录当前结果为5*2=10(因为已经弹出的5,6是升序的)。s={1},result = 10
2比1大,将弹出的5,6替换为2重新进栈。s={1,1,2,2,2},result = 10 注:这里s事实上只存储了1,2的下表,可以恢复它们的位置,这里为了方便理解,就写出来直观的意思了。
(6)3比2大,满足升序条件,进栈。s={1,1,2,2,2,3},result = 10
栈构建完成,满足升序条件,因此按照升序处理办法得到上述的max(height[i]*(size-i))=max{3*1, 2*2, 2*3, 2*4, 1*5, 1*6}=8<10
综上所述,result=10
在代码中,与上面的描述有两点不同,一是栈s存储的是数组下标的索引,二是在直方图末尾增加一个0作为哨兵,方便计算最后一个bar引起的面积(0可以使所有元素出栈,也就是上面第六步中的最后计算)。
代码
class Solution {
public:
int largestRectangleArea(vector<int>& heights) {
int res = 0;
stack<int> si;
heights.push_back(0); // NIL
const int n = heights.size();
for (int i = 0; i < n; ++i){
while (!si.empty() && heights[si.top()] >= heights[i]){
int h = heights[si.top()];
si.pop();
int s = h * (si.empty() ? i : (i - si.top() - 1));
res = max(res, s);
}
si.push(i);
}
return res;
}
};