SRDCF是在DCF/KCF的基础上,对目标函数正则化项进行改进,使用空间正则化惩罚来改进效果。SRDCF的Paper上关于数学推导部分非常多,但是其中仍有许多细节影响我们阅读代码。本来自己做了一份ppt,但是Google了下,发现有作者本人presentation的ppt关于细节部分非常详尽,于是直接用作者的ppt了,下面开始学习吧。
直接看ppt吧,博主不废话,只在关键地方中文解释。


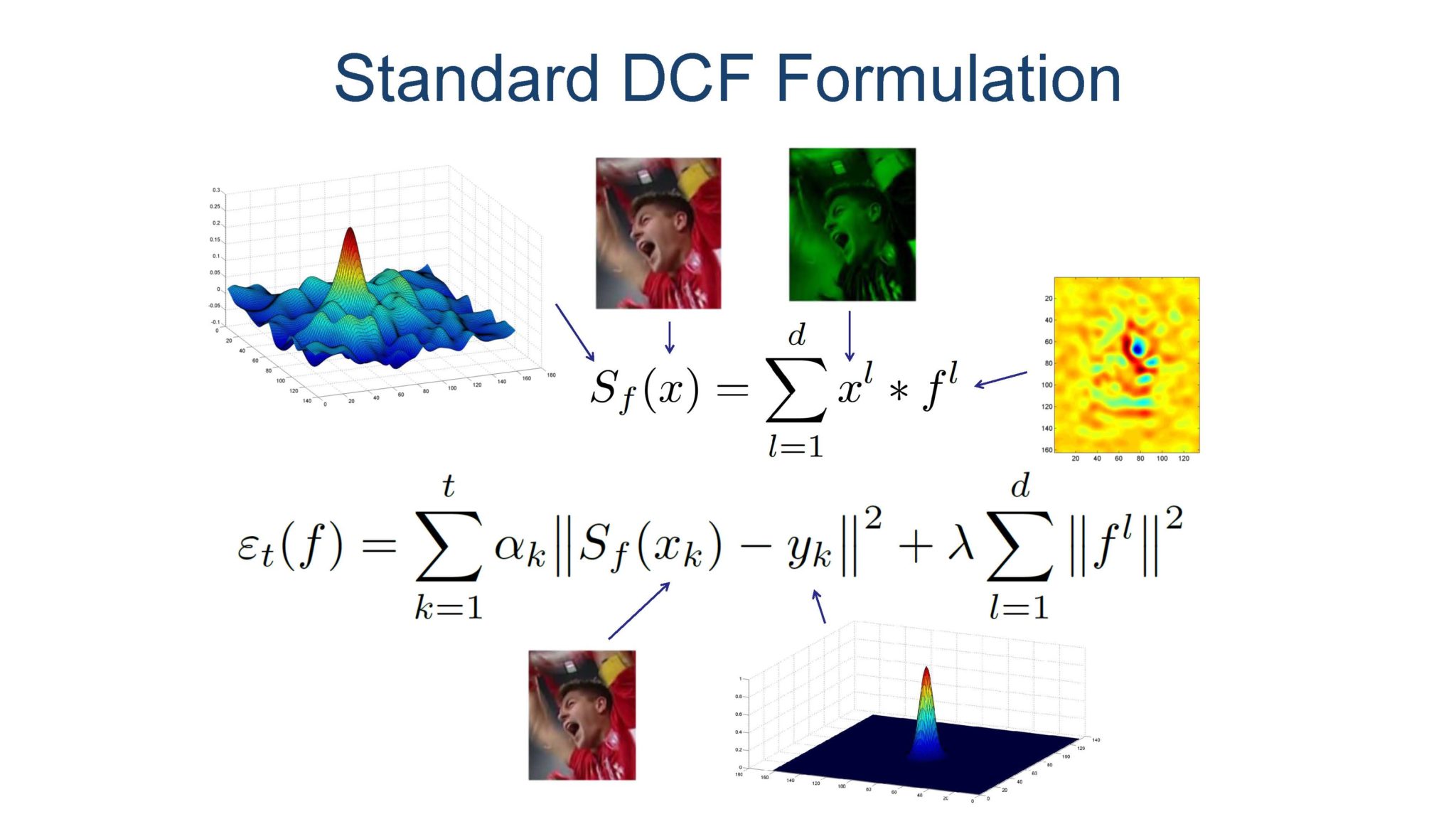
这张ppt是对KCF的形象解释,先看第二个方程,这个方程是在优化目标函数,也就是训练过程,得到f,也就是滤波器,其中l是通道,x是样本,y是希望得到的响应,最终优化出的是f,也就是滤波处理的滤波器。
然后看第一个方程,这是在做预测,Sf为最终的响应,f为许梿得到的滤波器,其中是在做卷积,实际上是通过傅里叶变换,在频域做点乘减小运算量的,最后在逆变换回来。



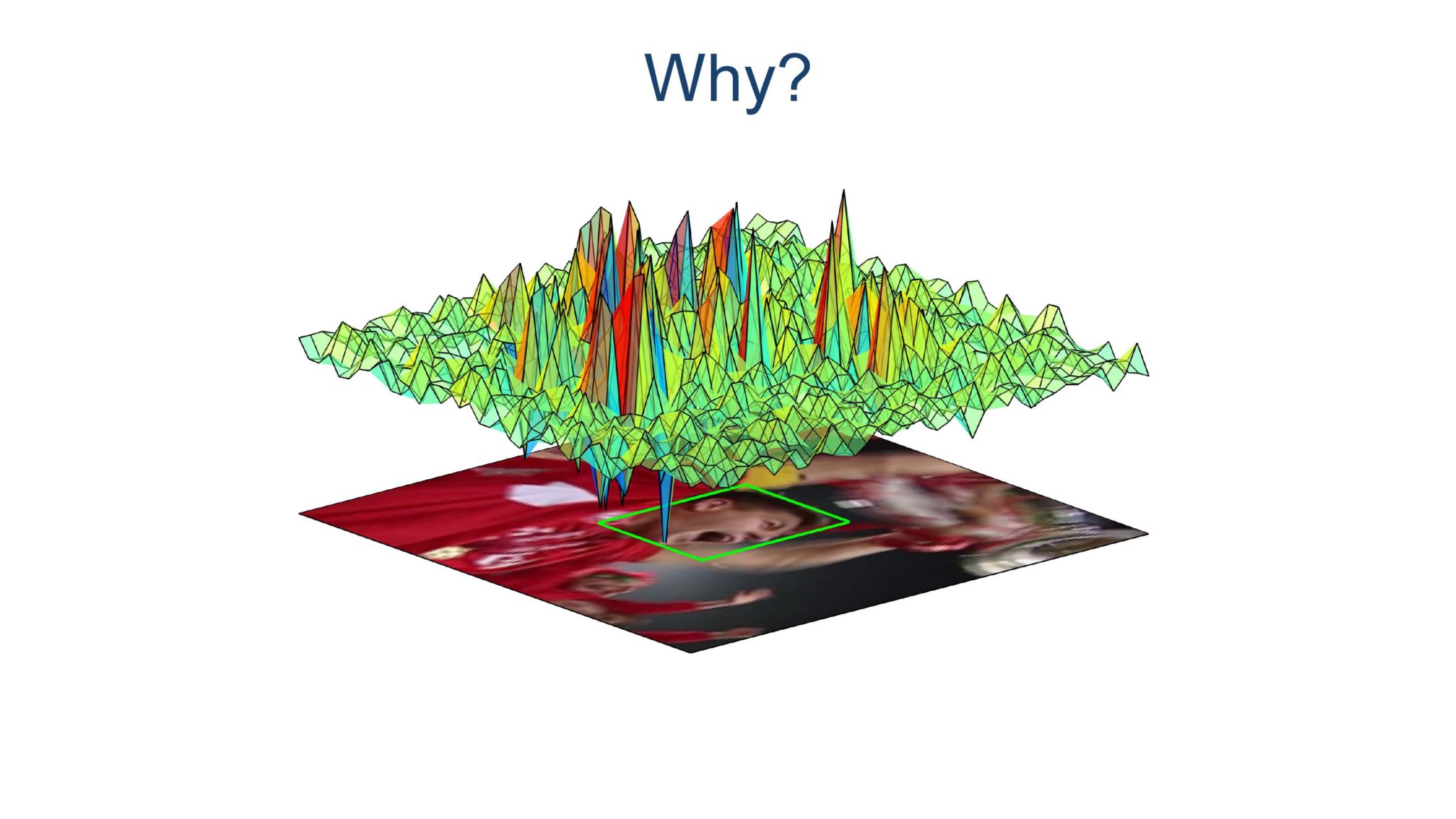
这就是在说,原来KCF算法的缺点,在非目标区域也存在着响应。

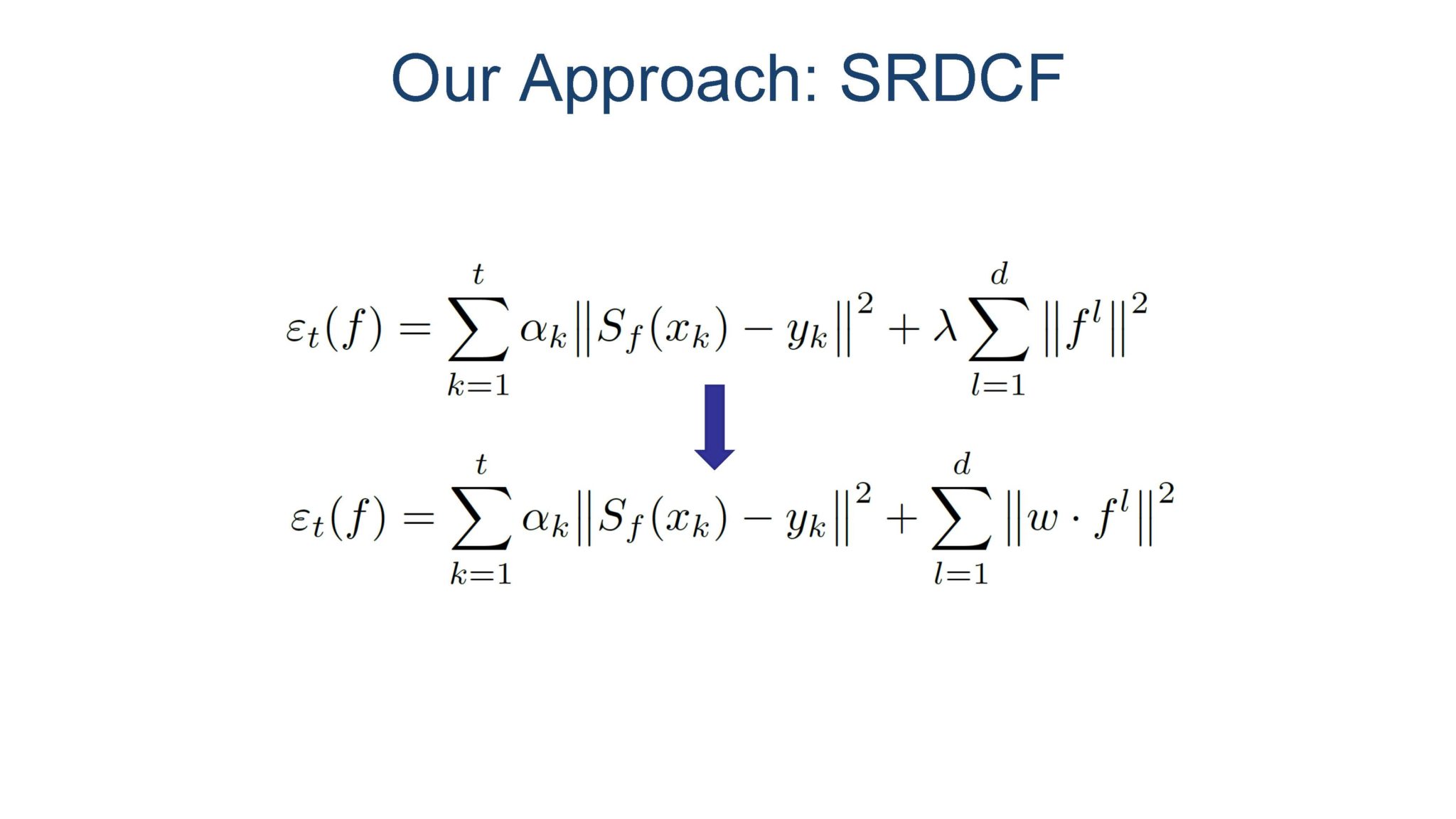
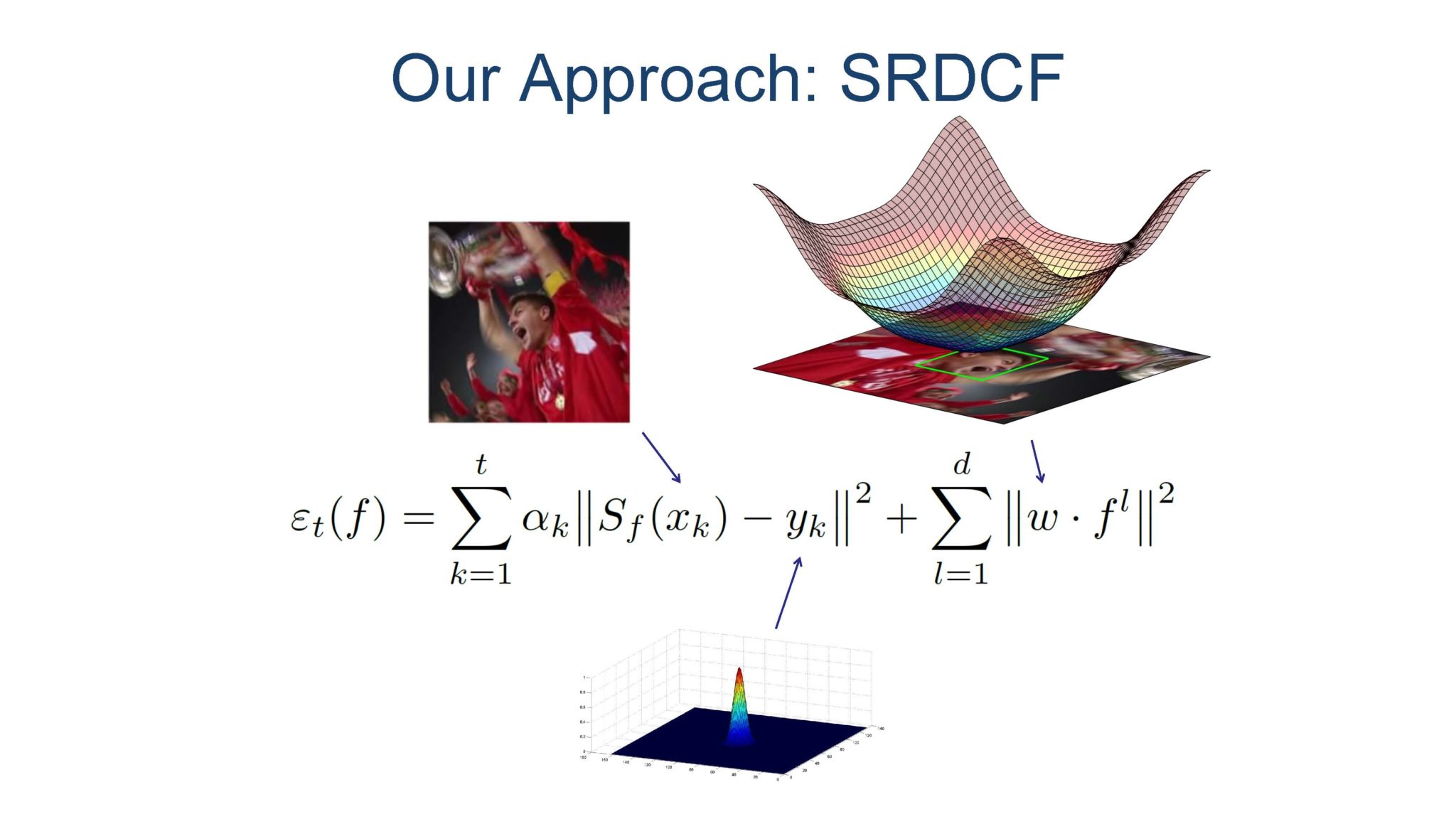
这就是在描述空间正则化,顾名思义,就是修改目标函数的正则化项,使得其能对空间靠边缘的部分产生抑制。

这个图很重要,因为Paper上没有,这也是很关键的一个分析:在W做离散傅里叶变换(DFT)之后,得到的矩阵是稀疏矩阵,在后面向量化之后,有个东西叫做强制稀疏,就和这个有关,后面几部使用的矩阵虽然很大,但是是稀疏的,很多很多地方是零。
如果看代码的话可以发现,这个地方变换之后,小于一个阈值的元素都被置零了(傅里叶变换之后,原本周边元素很小,单不完全等于零,现在将其近似为零),这也就是强制稀疏。

这个地方,就是从上往下,注意第二行到x,f,y的字体变了,这是在做向量化,第三行Paper中有描述,这是再向量化之后,用矩阵乘法来描述的向量化。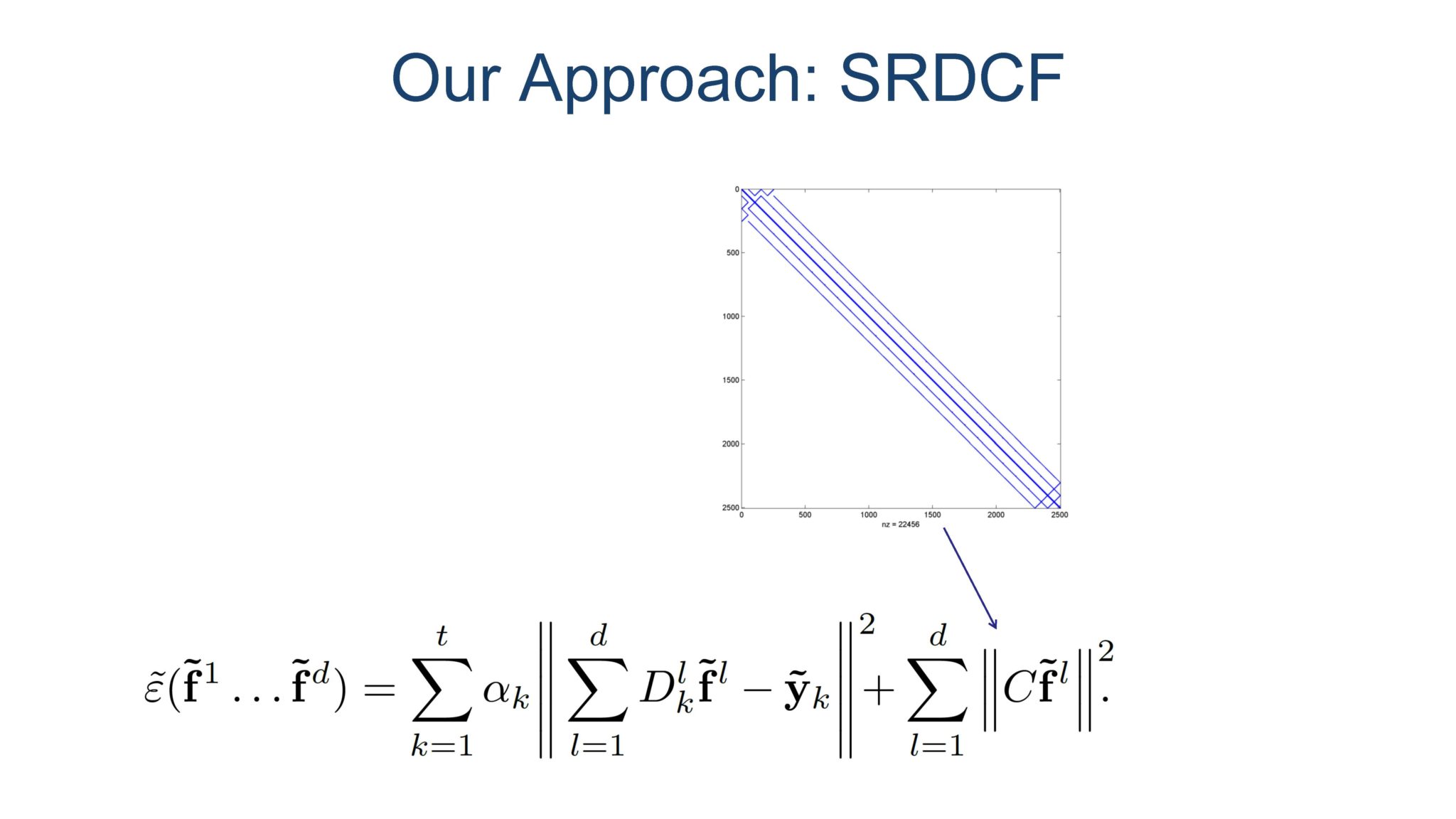
矩阵乘法描述的向量化中,C矩阵是稀疏的,这和前面的强制稀疏相互对应。
问题就被转化为一个方程参数求解的问题了。



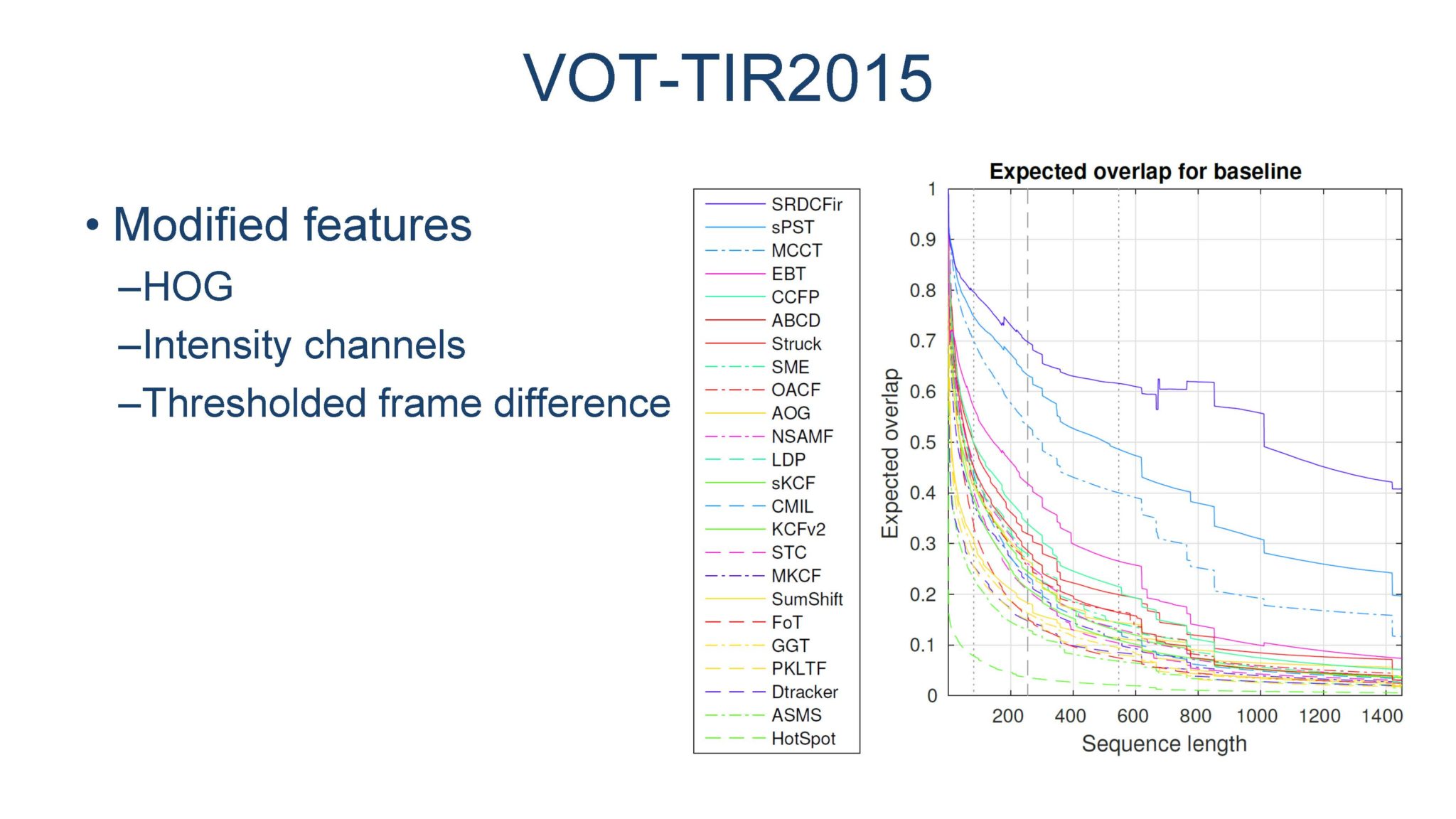
展示下效果,后面就是BenchMark评测了。


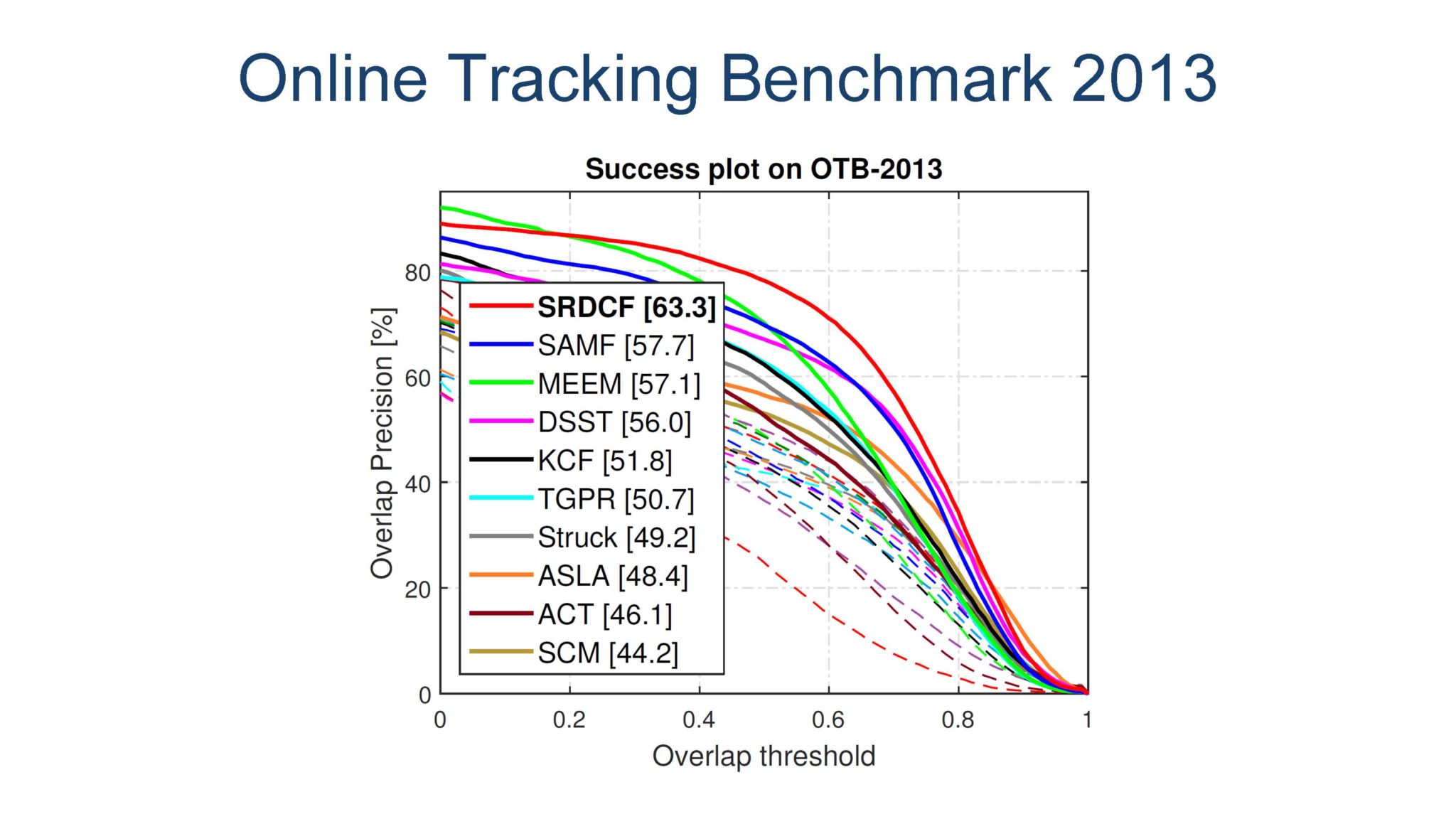
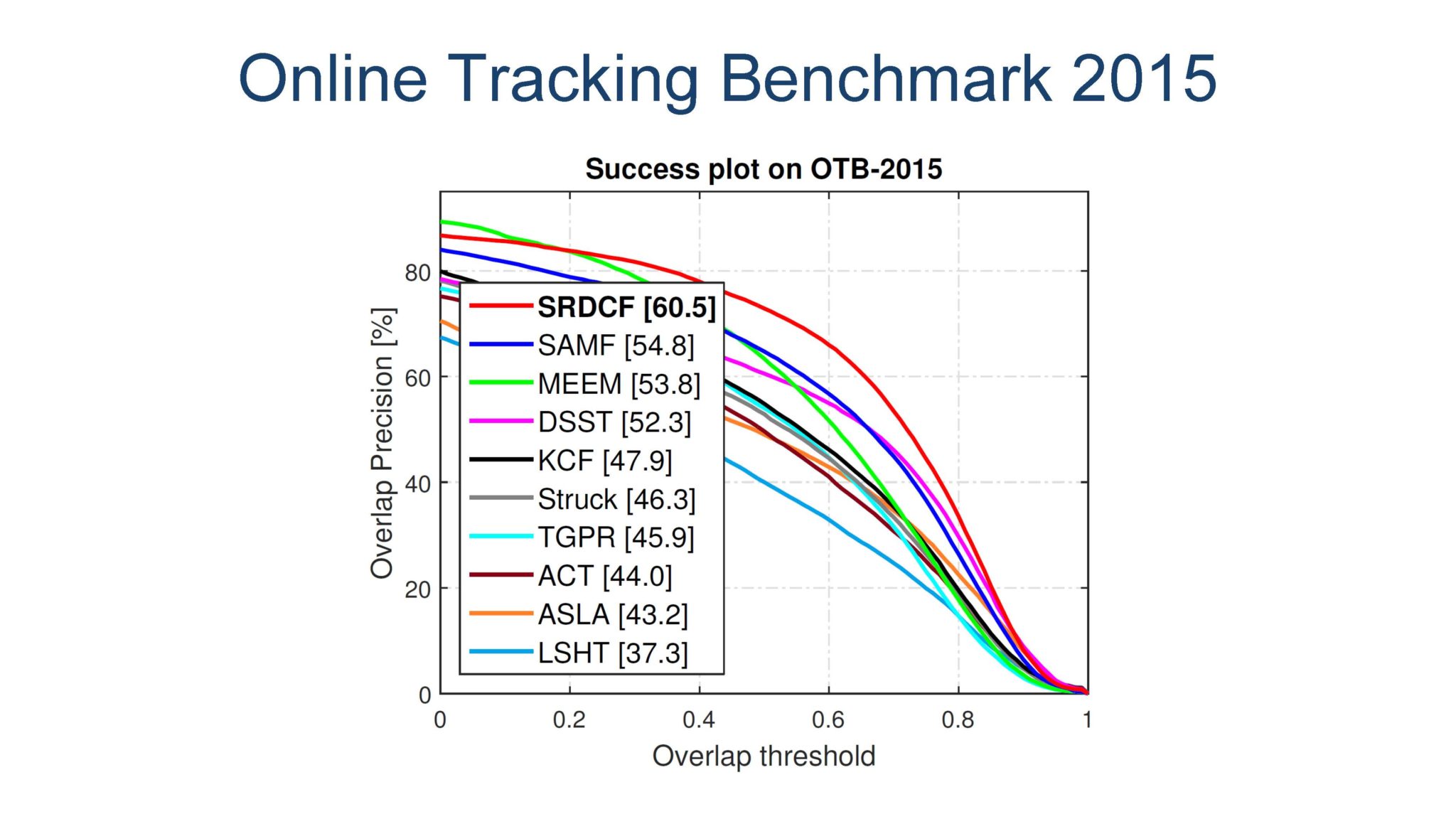


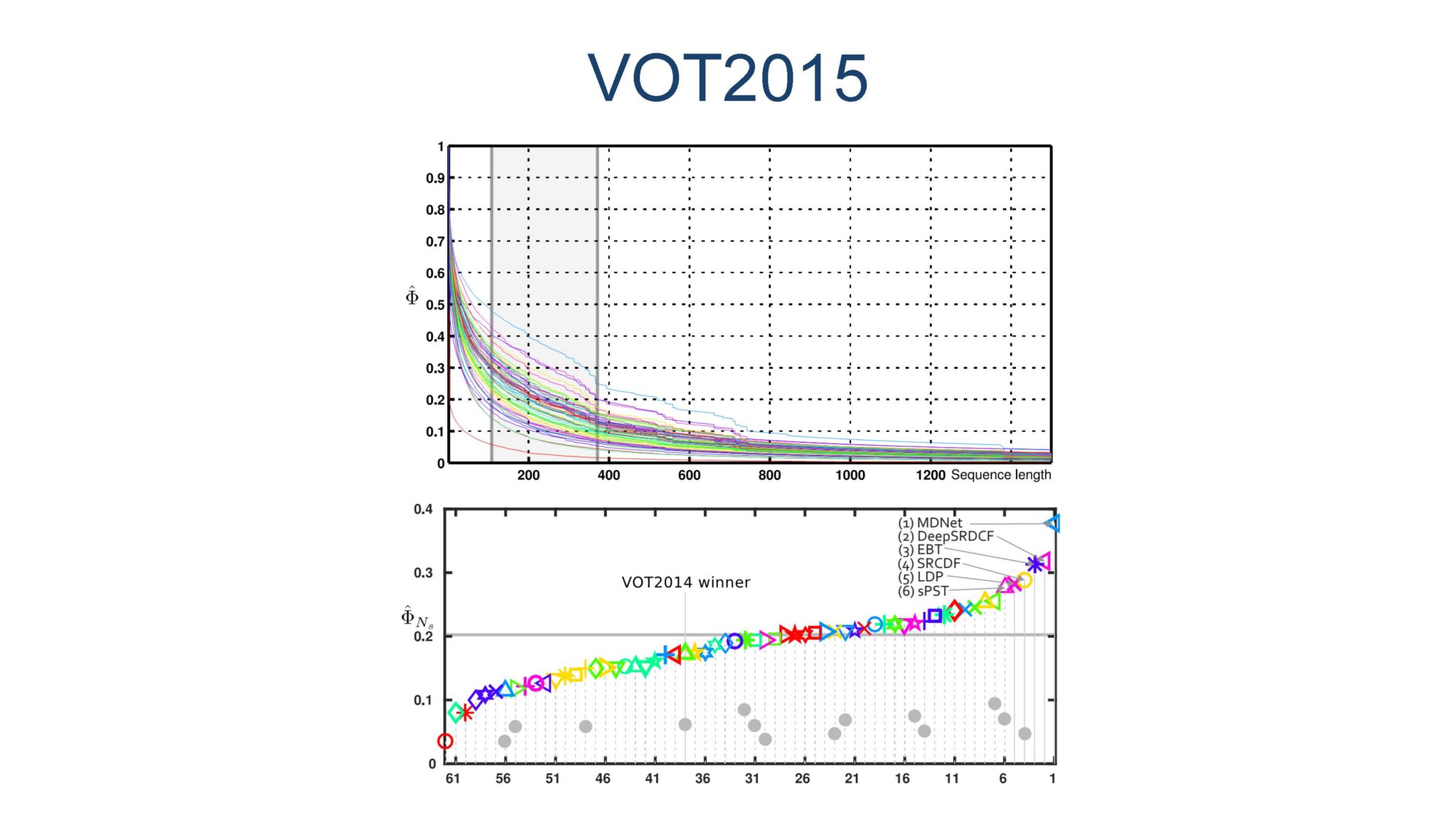
OK,See You Next Chapter!
ppt的下载地址能给一下吗?谢谢
http://data.votchallenge.net/vot2015/presentations/presentation_Danelljan.pdf
博主你好,请问这个ppt您是在哪里下载的