图像配准的方法大致分为三类,一类是基于灰度和模板的,这类方法直接采用相关运算等方式计算相关值来寻求最佳匹配位置,方法简单较为死板,一般效果不会太好。第二类是基于特征的匹配方法,如sift、surf点特征,或者向量特征等等,适应性较强。第三类是基于域变换的方法,采用相位相关(傅里叶-梅林变换)或者沃尔什变换、小波等方法,在新的域下进行配准。
我之前的博客介绍过傅里叶-梅林变换进行图像配准,其实也就是基于相位相关的原理,结合对数-极坐标变换进行图像配准,并给出了源码。这篇博客是对以上三类方法的小总结,无源码,都是废话,见谅。
1. 基于模板匹配的图像配准

模板匹配时图像配准算法中简单而常见的算法。在模板匹配中对图像的配准有整幅图像进行的撇皮,也有局部图像和局部图像之间进行的匹配。在模板匹配过程中通常对模板进行平移,计算对应关系。一般情况下,采用模板和图像的相关运算计算相关值,相关值越大表示匹配越好。
模板匹配对形态固定的图案具有较好的效果,但是随着配准图像在数量级的扩大,计算复杂度会增加,实时性会增加,随着图像拍摄环境和成像条件的多变,算法的适应性会变差。
2. 基于灰度的图像配准
灰度图像配准是利用灰度信息来测量图像的相同部分,方法简单,但是对目标的变动和扭曲会影响配准效果。较为常见的是求其相似性代价函数,将图像的灰度差做平方和运算。
灰度图像配准方法不需要提取图像的几何特征,所以有很高的识别精度和适用性,单也因为图像灰度信息鼠标比较大,因此运算量大,效率低。
3. 相位相关法、傅里叶-梅林变换(基于变换域的方法)

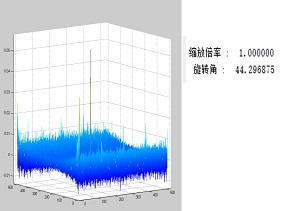
基于变换域的方法有很多,这里安利下我之前的博客:傅里叶-梅林变换进行图像配准 ,也就是采用了基于相位相关的方法进行的,博客中给出了Matlab的源码。
相位相关法师对图像进行参数转换,利用转换后的参数进行运算,图像由参数变换转换到频域,利用傅里叶变换得到平移后的结果,再在频域实现匹配图像的配准。在傅里叶变换后,图像的平移成分转换到了相位,计算相位的最大匹配位置,就可以得到原始图像的平移量了,这就是相位相关。
更进一步,我们引入傅里叶-梅林变换的概念。我们通过相位相关只能得到平移量,那么如果有旋转和缩放呢?是否还记得传统图像中的对数-极坐标变换呢?
没错,将二者结合起来:相位相关得到平移位置,对数变换得到尺度,极坐标变换得到旋转角,这就是傅里叶-梅林变换。更详细的说明,参见我原先的博客吧。
4. 基于模型的图像配准
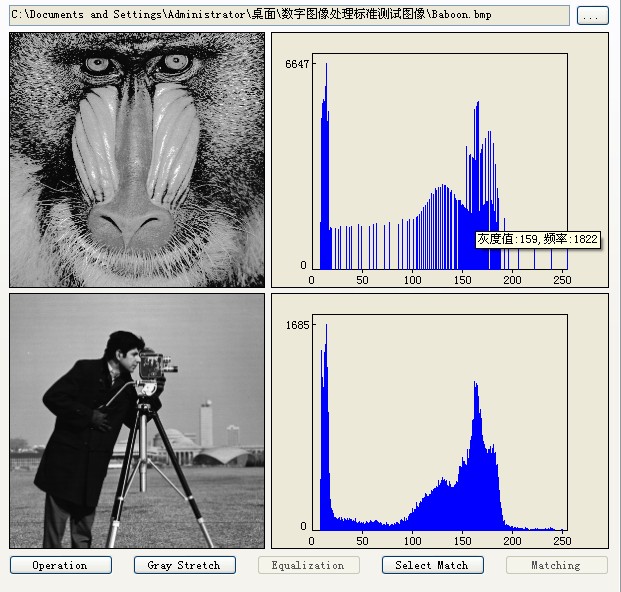
基于模型的配准方法是依据数学模型进行对比,并且可以通过对比度来进行图像配准分析。首先对序列图像建立数据模型,之后以迭代求解出相关模型之间对应的相关未知量,最后通过这些计算出的未知量对图像进行配准。
这类方法的优点在于可以快读的进行序列图像间的水平移动、扭曲、拓展和收缩等形状变化,统计效果很好。缺点在于使用此方法有整体优良的收敛效果,需要有一个好的初始配准估计值,否则会匹配失败。
5. 基于特征的图像配准

这类方法首先分析两幅待配准图像,提取特征域,在特征域进行匹配,根据特征域计算得到特征向量。这里要提到,特征分为点特征(如sift、surf等)、线特征、统计特征等等。这类方法依据使用的特征不同,会表现出不同的效果。比较经典的配准方式是SURF特征+Ransac筛选,得到匹配点对坐标来计算图像变换参数。
6. 消除误匹配算法
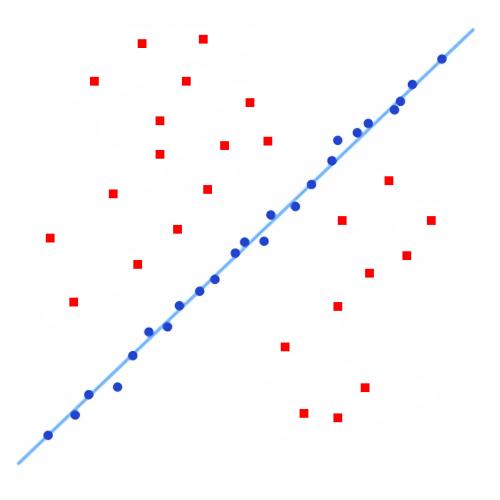
使用任何类型的匹配算法,匹配误差都是不可避免的,处于初始匹配结果后有大量的异常点,这些异常点可以通过随机抽样一致性算法(Random Sample Consensus,也就是我们常说的Ransac)来消除误匹配。Ransac是一种不确定和随机的算法,每次运算得到的结果可能会不同,但其具有有效的整体估计效果,即使匹配失败超过50%的数据,仍然能得到合理的结果。