ECC增强相关系数图像配准

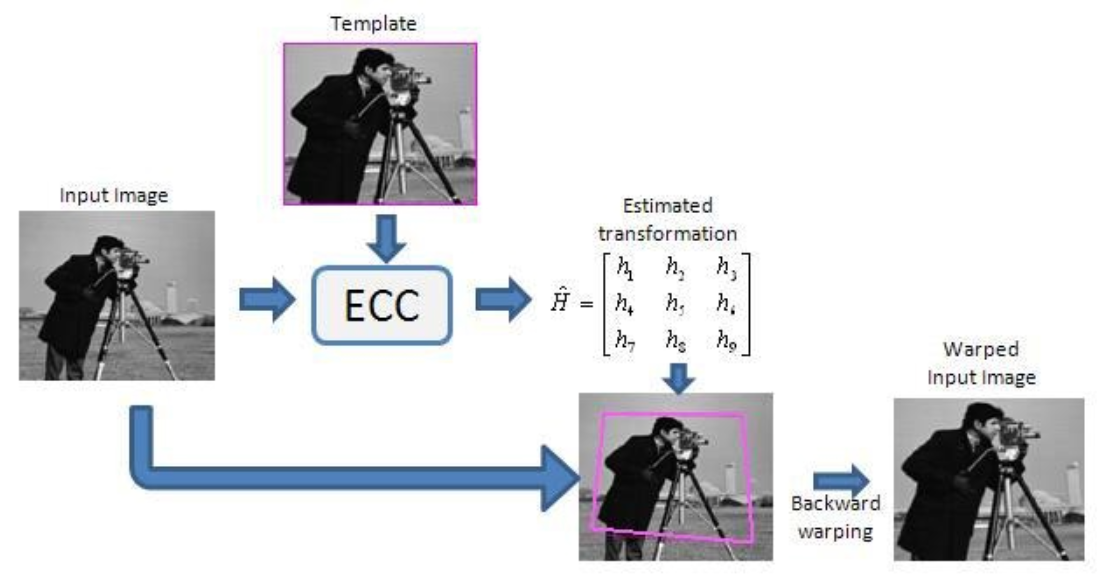
传统图像配准算法有基于特征点、变换域、参数求解几种，其中参数求解算法中，ECC具有很好的速度和硬件友好的实现，这篇博客会看下论文推导和opencv的开源实现。

〇、论文下载：

ECC论文有两篇paper，博主截图VISAPP_2018这篇paper的，PAMI里面推导更加详细，一般看PAMI这篇就可以了。

一、ECC迭代推导

参数化的图像配置问题可以被表示为，减少warp图像经过参数p warp和经过alpha光照恒常补偿后和参考图像误差。

我们将图像Ir和Iw都减去均值，除以norm2范数（进行归一化），就散Ir和Iw(p)之间的偏差。现在的问题就是最小化这个Error。

最小化Eecc的过程也可以被转化为最大化rho(p)的过程，rho(p)就是增强相关系数

我们最大化pho(p)，p=bar_p+delta_p的过程表达出来，然后进行泰勒展开，泰勒我们只取一阶近似，可以展开成如下公式

可以看到，这样公式中已经和p没有关系了，只和delta_p 还有 G （梯度）有关系，这样有什么好处呢？就是我们知道梯度的话，就可以迭代求解rho(p)的最大值，这和传统光流很像。

寻找delta_p使得前面公式的值最大，这个问题已经被证明是有解析解的，这里解有两种情况：

第一种情况直接可以写出解析解（opencv种只实现了这第一种情况，式8和式9）

第二种情况，我们没办法明确给出解析解，只能知道解的范围

（这部分推导在PAMI2018哪个paper里面写的详细点儿，附录里有推导）

通过推到rho关于lambda的单调性，可以得到下面两个不等式，对于lamda>lamda1的情况，rho>rho(0), 对于lamda>=lamda2的情况，rho>=0，所以可以知道lambda的上界

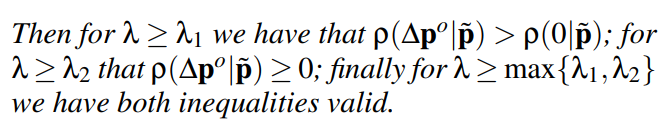
我们重新回来看我们配准过程中的迭代问题，依旧是把参数进行泰勒展开

其中T(p)的jacobian根据变换参数类型不同可以写成不同的形式，对于仿射变换而言，dT/dp 可以写成下面的矩阵

那么ECC的迭代过成可以做如果表述：

二、开源源码解读

接下来我们看下opencv中的ecc源码（全部源码位于video模块中的ecc.cpp），实现还是非常简洁的。关于源码的理解：

1. 代码中都是矩阵乘法等并行操作，很适合GPU或者DSP等做并行加速。
2. opencv源码中可以输出error，如果不需要输出error，把error的表达带入error_projection的计算中，error_projection可以直接由lambda、image_projection和template_projection得到，可以减少一些计算量。
3. 输入可以配mask，不要mask的话可以去掉，也有优化不少时间
4. opencv的代码中直接使用了论文中 第一种情况下的解，对第二种情况下的解，opencv 直接 throw error，并未对第二种解单独处理，这一点博主这还没有理解透彻，有理解的小伙伴可以留言告诉博主

double cv::findTransformECC(InputArray templateImage,
                            InputArray inputImage,
                            InputOutputArray warpMatrix,
                            int motionType,
                            TermCriteria criteria,
                            InputArray inputMask,
                            int gaussFiltSize)
{


    Mat src = templateImage.getMat();//template image
    Mat dst = inputImage.getMat(); //input image (to be warped)
    Mat map = warpMatrix.getMat(); //warp (transformation)

    CV_Assert(!src.empty());
    CV_Assert(!dst.empty());

    // If the user passed an un-initialized warpMatrix, initialize to identity
    if(map.empty()) {
        int rowCount = 2;
        if(motionType == MOTION_HOMOGRAPHY)
            rowCount = 3;

        warpMatrix.create(rowCount, 3, CV_32FC1);
        map = warpMatrix.getMat();
        map = Mat::eye(rowCount, 3, CV_32F);
    }

    if( ! (src.type()==dst.type()))
        CV_Error( Error::StsUnmatchedFormats, "Both input images must have the same data type" );

    //accept only 1-channel images
    if( src.type() != CV_8UC1 && src.type()!= CV_32FC1)
        CV_Error( Error::StsUnsupportedFormat, "Images must have 8uC1 or 32fC1 type");

    if( map.type() != CV_32FC1)
        CV_Error( Error::StsUnsupportedFormat, "warpMatrix must be single-channel floating-point matrix");

    CV_Assert (map.cols == 3);
    CV_Assert (map.rows == 2 || map.rows ==3);

    CV_Assert (motionType == MOTION_AFFINE || motionType == MOTION_HOMOGRAPHY ||
        motionType == MOTION_EUCLIDEAN || motionType == MOTION_TRANSLATION);

    if (motionType == MOTION_HOMOGRAPHY){
        CV_Assert (map.rows ==3);
    }

    CV_Assert (criteria.type & TermCriteria::COUNT || criteria.type & TermCriteria::EPS);
    const int    numberOfIterations = (criteria.type & TermCriteria::COUNT) ? criteria.maxCount : 200;
    const double termination_eps    = (criteria.type & TermCriteria::EPS)   ? criteria.epsilon  :  -1;

    int paramTemp = 6;//default: affine
    switch (motionType){
      case MOTION_TRANSLATION:
          paramTemp = 2;
          break;
      case MOTION_EUCLIDEAN:
          paramTemp = 3;
          break;
      case MOTION_HOMOGRAPHY:
          paramTemp = 8;
          break;
    }


    const int numberOfParameters = paramTemp;

    const int ws = src.cols;
    const int hs = src.rows;
    const int wd = dst.cols;
    const int hd = dst.rows;

    Mat Xcoord = Mat(1, ws, CV_32F);
    Mat Ycoord = Mat(hs, 1, CV_32F);
    Mat Xgrid = Mat(hs, ws, CV_32F);
    Mat Ygrid = Mat(hs, ws, CV_32F);

    float* XcoPtr = Xcoord.ptr<float>(0);
    float* YcoPtr = Ycoord.ptr<float>(0);
    int j;
    for (j=0; j<ws; j++)
        XcoPtr[j] = (float) j;
    for (j=0; j<hs; j++)
        YcoPtr[j] = (float) j;

    repeat(Xcoord, hs, 1, Xgrid);
    repeat(Ycoord, 1, ws, Ygrid);

    Xcoord.release();
    Ycoord.release();

    Mat templateZM    = Mat(hs, ws, CV_32F);// to store the (smoothed)zero-mean version of template
    Mat templateFloat = Mat(hs, ws, CV_32F);// to store the (smoothed) template
    Mat imageFloat    = Mat(hd, wd, CV_32F);// to store the (smoothed) input image
    Mat imageWarped   = Mat(hs, ws, CV_32F);// to store the warped zero-mean input image
    Mat imageMask     = Mat(hs, ws, CV_8U); // to store the final mask

    Mat inputMaskMat = inputMask.getMat();
    //to use it for mask warping
    Mat preMask;
    if(inputMask.empty())
        preMask = Mat::ones(hd, wd, CV_8U);
    else
        threshold(inputMask, preMask, 0, 1, THRESH_BINARY);

    //gaussian filtering is optional
    src.convertTo(templateFloat, templateFloat.type());
    GaussianBlur(templateFloat, templateFloat, Size(gaussFiltSize, gaussFiltSize), 0, 0);

    Mat preMaskFloat;
    preMask.convertTo(preMaskFloat, CV_32F);
    GaussianBlur(preMaskFloat, preMaskFloat, Size(gaussFiltSize, gaussFiltSize), 0, 0);
    // Change threshold.
    preMaskFloat *= (0.5/0.95);
    // Rounding conversion.
    preMaskFloat.convertTo(preMask, preMask.type());
    preMask.convertTo(preMaskFloat, preMaskFloat.type());

    dst.convertTo(imageFloat, imageFloat.type());
    GaussianBlur(imageFloat, imageFloat, Size(gaussFiltSize, gaussFiltSize), 0, 0);

    // needed matrices for gradients and warped gradients
    Mat gradientX = Mat::zeros(hd, wd, CV_32FC1);
    Mat gradientY = Mat::zeros(hd, wd, CV_32FC1);
    Mat gradientXWarped = Mat(hs, ws, CV_32FC1);
    Mat gradientYWarped = Mat(hs, ws, CV_32FC1);


    // calculate first order image derivatives
    Matx13f dx(-0.5f, 0.0f, 0.5f);

    filter2D(imageFloat, gradientX, -1, dx);
    filter2D(imageFloat, gradientY, -1, dx.t());

    gradientX = gradientX.mul(preMaskFloat);
    gradientY = gradientY.mul(preMaskFloat);

    // matrices needed for solving linear equation system for maximizing ECC
    Mat jacobian                = Mat(hs, ws*numberOfParameters, CV_32F);
    Mat hessian                 = Mat(numberOfParameters, numberOfParameters, CV_32F);
    Mat hessianInv              = Mat(numberOfParameters, numberOfParameters, CV_32F);
    Mat imageProjection         = Mat(numberOfParameters, 1, CV_32F);
    Mat templateProjection      = Mat(numberOfParameters, 1, CV_32F);
    Mat imageProjectionHessian  = Mat(numberOfParameters, 1, CV_32F);
    Mat errorProjection         = Mat(numberOfParameters, 1, CV_32F);

    Mat deltaP = Mat(numberOfParameters, 1, CV_32F);//transformation parameter correction
    Mat error = Mat(hs, ws, CV_32F);//error as 2D matrix

    const int imageFlags = INTER_LINEAR  + WARP_INVERSE_MAP;
    const int maskFlags  = INTER_NEAREST + WARP_INVERSE_MAP;


    // iteratively update map_matrix
    double rho      = -1;
    double last_rho = - termination_eps;
    for (int i = 1; (i <= numberOfIterations) && (fabs(rho-last_rho)>= termination_eps); i++)
    {

        // warp-back portion of the inputImage and gradients to the coordinate space of the templateImage
        if (motionType != MOTION_HOMOGRAPHY)
        {
            warpAffine(imageFloat, imageWarped,     map, imageWarped.size(),     imageFlags);
            warpAffine(gradientX,  gradientXWarped, map, gradientXWarped.size(), imageFlags);
            warpAffine(gradientY,  gradientYWarped, map, gradientYWarped.size(), imageFlags);
            warpAffine(preMask,    imageMask,       map, imageMask.size(),       maskFlags);
        }
        else
        {
            warpPerspective(imageFloat, imageWarped,     map, imageWarped.size(),     imageFlags);
            warpPerspective(gradientX,  gradientXWarped, map, gradientXWarped.size(), imageFlags);
            warpPerspective(gradientY,  gradientYWarped, map, gradientYWarped.size(), imageFlags);
            warpPerspective(preMask,    imageMask,       map, imageMask.size(),       maskFlags);
        }

        Scalar imgMean, imgStd, tmpMean, tmpStd;
        meanStdDev(imageWarped,   imgMean, imgStd, imageMask);
        meanStdDev(templateFloat, tmpMean, tmpStd, imageMask);

        subtract(imageWarped,   imgMean, imageWarped, imageMask);//zero-mean input
        templateZM = Mat::zeros(templateZM.rows, templateZM.cols, templateZM.type());
        subtract(templateFloat, tmpMean, templateZM,  imageMask);//zero-mean template

        const double tmpNorm = std::sqrt(countNonZero(imageMask)*(tmpStd.val[0])*(tmpStd.val[0]));
        const double imgNorm = std::sqrt(countNonZero(imageMask)*(imgStd.val[0])*(imgStd.val[0]));

        // calculate jacobian of image wrt parameters
        switch (motionType){
            case MOTION_AFFINE:
                image_jacobian_affine_ECC(gradientXWarped, gradientYWarped, Xgrid, Ygrid, jacobian);
                break;
            case MOTION_HOMOGRAPHY:
                image_jacobian_homo_ECC(gradientXWarped, gradientYWarped, Xgrid, Ygrid, map, jacobian);
                break;
            case MOTION_TRANSLATION:
                image_jacobian_translation_ECC(gradientXWarped, gradientYWarped, jacobian);
                break;
            case MOTION_EUCLIDEAN:
                image_jacobian_euclidean_ECC(gradientXWarped, gradientYWarped, Xgrid, Ygrid, map, jacobian);
                break;
        }

        // calculate Hessian and its inverse
        project_onto_jacobian_ECC(jacobian, jacobian, hessian);

        hessianInv = hessian.inv();

        const double correlation = templateZM.dot(imageWarped);

        // calculate enhanced correlation coefficient (ECC)->rho
        last_rho = rho;
        rho = correlation/(imgNorm*tmpNorm);
        if (cvIsNaN(rho)) {
          CV_Error(Error::StsNoConv, "NaN encountered.");
        }

        // project images into jacobian
        project_onto_jacobian_ECC( jacobian, imageWarped, imageProjection);
        project_onto_jacobian_ECC(jacobian, templateZM, templateProjection);


        // calculate the parameter lambda to account for illumination variation
        imageProjectionHessian = hessianInv*imageProjection;
        const double lambda_n = (imgNorm*imgNorm) - imageProjection.dot(imageProjectionHessian);
        const double lambda_d = correlation - templateProjection.dot(imageProjectionHessian);
        if (lambda_d <= 0.0)
        {
            rho = -1;
            CV_Error(Error::StsNoConv, "The algorithm stopped before its convergence. The correlation is going to be minimized. Images may be uncorrelated or non-overlapped");

        }
        const double lambda = (lambda_n/lambda_d);

        // estimate the update step delta_p
        error = lambda*templateZM - imageWarped;
        project_onto_jacobian_ECC(jacobian, error, errorProjection);
        deltaP = hessianInv * errorProjection;

        // update warping matrix
        update_warping_matrix_ECC( map, deltaP, motionType);


    }

    // return final correlation coefficient
    return rho;
}