量化投资（五）期权跨式组合

前面博客介绍了期权四个基本交易方向，在此基础上，我们看一些期权的交易策略。

在期权交易中，我们不仅可以做多（做空）股价，还可以做多（做空）波动率。跨式组合（straddle）和宽跨式组合（strangle）是较为常用的手段。这篇博客介绍 straddle 和 strangle 交易策略 和 Python绘制收益曲线。

跨式组合

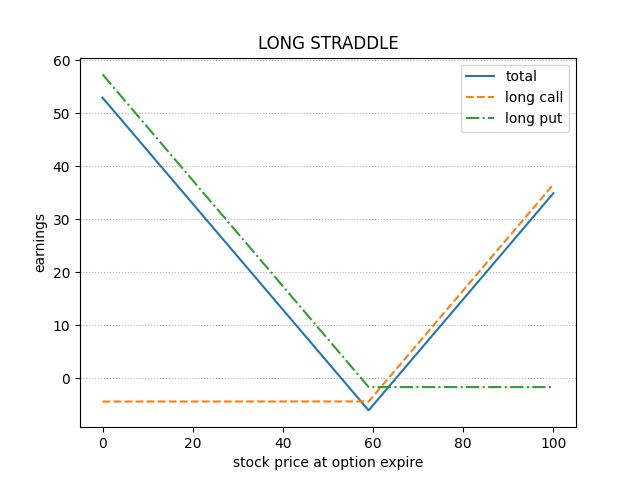
买入跨式组合，即买入到期日相同，行权价格相同的看涨期权（LONG CALL）和看跌期权（LONG PUT），这样我们可以实现下面的收益曲线：

不论标的涨跌，只要 long call 或者 long put 任何一边可以实现盈利，且盈利超过我们支出的两份期权权利金，我们即可以实现组合的盈利。所以，到期日之前，只要股价波动超过一定幅度，组合即可以实现盈利。

需要注意：

1. 期权价格不能过高或者过低，以保证足够的利润
2. 未来的事件可以显著影响股价
3. 未来的事件发生后至少三十天后期权才到期，以便坚持到事件发生之后平仓。因为在快到期时期权时间价值缩减的很厉害，如果迟迟没有发生事件持仓压力很大
4. 未来的事件在目前来说不算大，比如9月份时美国大选就不是个很大的事
5. 在某些时候（比如有一致预期的），在事件发生之前可以平盈利的leg，因为一般这种都是事件发生前顺预期走，发生之后如果符合预期则反向走，此时可以平掉剩下亏损的leg
6. 在事件发生之后尽快平仓，趁着这时候时间价值因为事件的原因大幅上调，之后可能会回落

除了买入跨式组合，我们还可以卖出跨式组合，以做空标的波动，这里就是把上面的图上下翻过来（沿着x轴上下翻转），这里不再赘述。

宽跨式组合

宽跨式组合是由跨式组合衍生过来的，它与跨式组合的区别是，LONG CALL和LONG PUT的行权价不同。我们通常选择更加虚值的CALL和PUT以降低成本，但是组合盈利也要求更大的波动率。

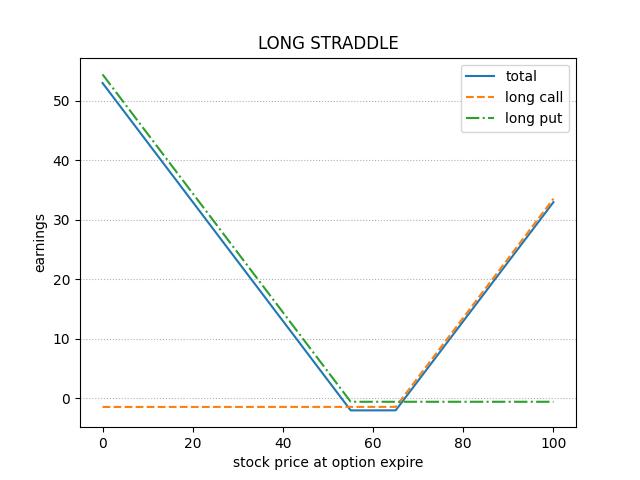
类似于卖出跨式组合，应用于投资者认为未来标的物价格波动较小，不会发生大幅情况，均属于做空波动率的交易策略。其中，卖出宽跨式组合比卖出跨式组合收到的权利金少，但可以确保其能够盈利的标的期货价格波动范围较宽。

代码

github仓库

代码比较简单：

import numpy as np
import matplotlib.pyplot as plt
from types import SimpleNamespace


class Option:
    def __init__(self, name, price):
        self.name = name
        self.stock = name
        self.price = price
        self.stock, _, self.exercise_price = name.split(' ')
        self.exercise_price = float(self.exercise_price)


def calc_option_earnings(tic_price, option, operation='long'):

    # exercise inner value
    value_option = tic_price
    if 'call' in option.name.lower():
        value_option = np.maximum(0, tic_price - option.exercise_price)
    if 'put' in option.name.lower():
        value_option = np.maximum(0, option.exercise_price - tic_price)
    if 'sell' in operation.lower() or 'short' in operation.lower():
        value_option = -value_option

    earnings = value_option - option.price

    return earnings


def test_straddle():
    tic_price = np.arange(0, 100, 0.01)

    option_call = Option("JD CALL 59", 4.40)
    option_put = Option('JD PUT 59', 1.67)

    long_call = calc_option_earnings(tic_price, option_call, 'LONG')
    long_put = calc_option_earnings(tic_price, option_put, 'LONG')

    plt.figure()
    plt.subplots_adjust(left=None, bottom=None, right=None, top=None,
                        wspace=0.1, hspace=0.0)
    plt.subplot(1, 2, 1)
    plt.plot(tic_price, long_call + long_put, label='total')
    plt.plot(tic_price, long_call, linestyle='--', label='long call')
    plt.plot(tic_price, long_put, linestyle='-.', label='long put')
    plt.legend()
    plt.title('LONG STRADDLE')
    plt.xlabel('stock price at option expire')
    plt.ylabel('earnings')
    plt.grid(axis='y', linestyle=':')


def test_strangle():
    tic_price = np.arange(0, 100, 0.01)

    option_call = Option("JD CALL 65", 1.45)
    option_put = Option('JD PUT 55', 0.58)

    long_call = calc_option_earnings(tic_price, option_call, 'LONG')
    long_put = calc_option_earnings(tic_price, option_put, 'LONG')

    plt.figure()
    plt.plot(tic_price, long_call + long_put, label='total')
    plt.plot(tic_price, long_call, linestyle='--', label='long call')
    plt.plot(tic_price, long_put, linestyle='-.', label='long put')
    plt.legend()
    plt.title('LONG STRADDLE')
    plt.xlabel('stock price at option expire')
    plt.ylabel('earnings')
    plt.grid(axis='y', linestyle=':')


if __name__ == "__main__":
    test_straddle()
    test_strangle()