图像降噪算法 Multi Scale DCT Denoise

Multi Scale DCT Denoise（MSDCT）是经典的传统降噪算法，这篇博客予以简单介绍。原始论文：https://www.ipol.im/pub/art/2017/201/article_lr.pdf， C++源码，可以在ipol网站找到：https://www.ipol.im/pub/art/2017/201/?utm_source=doi

DCT变换

DCT变换是DFT变换的一种特殊形式，在介绍DCT之前，我们先看下DFT了，离散余弦变换DCT和离散傅立叶变换DFT一样，都是将信号变换到其它基下进行表示，只不过变换选取的基空间不同。

DCT与DFT有诸多联系，在介绍DCT之前，我们回顾下DFT的变换公式

X[k]=\sum_{n=0}^{N-1}x[n](\cos(\frac{2\pi kn}{N}-j\sin(\frac{2\pi kn}{N})))

DFT变换的结果分为实数部分和虚数部分。实数部分 cos 是个偶函数，虚数部分 sin 是个奇函数。我们假设原始信号 [latax]x[n][/latex] 是一个全是实数的偶函数，那么实部依然是个偶函数，虚部依然是个奇函数，此时变换信号的虚部为0

Im[k]=\sum_{n=-（N-1）}^{N-1}x[n](\sin\frac{2\pi kn}{N})=0 \ \ \ \ \ \ \ \ \ while\ x[n]=x[-n]

到这里我们已经接近DCT变换的核心了，DCT变换就是限定了输入信号的DFT变换，我们看下DCT变换的公式

F(u)=c(u)\sum_{x=0}^{N-1}f(x)\cos(\frac{(x+0.5)\pi}{N}u) \\ c(0) = \sqrt{\frac{1}{N}} \ \ \ \ otherwise \ \ \ c(u)=\sqrt{\frac{2}{N}}

我们可以看出来，DCT变换就是输入是实偶信号的DFT变换，但是实际应用中如果没有实偶信号，哦我们呢需要构造一个实偶信号。我们把原始信号做镜像和平移就可以构造这样一个函数了，这也是上述公式中 $(x+0.5)\pi$ 这一项的由来。

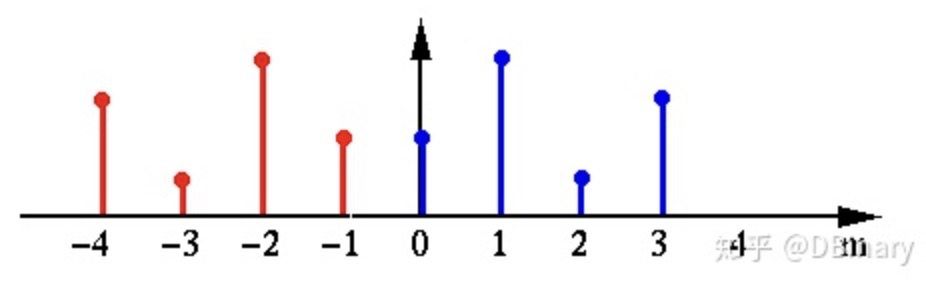
信号经过平移0.5之后就是完全的偶函数了。

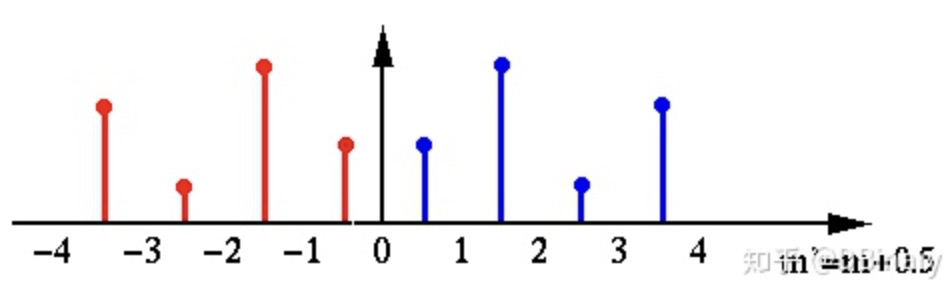
那么相比于DFT，DCT好处在哪里呢？一个是DCT能量集中在实部低频（变换图像左上角），更有利于信号的压缩，另一个是变换速度更快更高效。

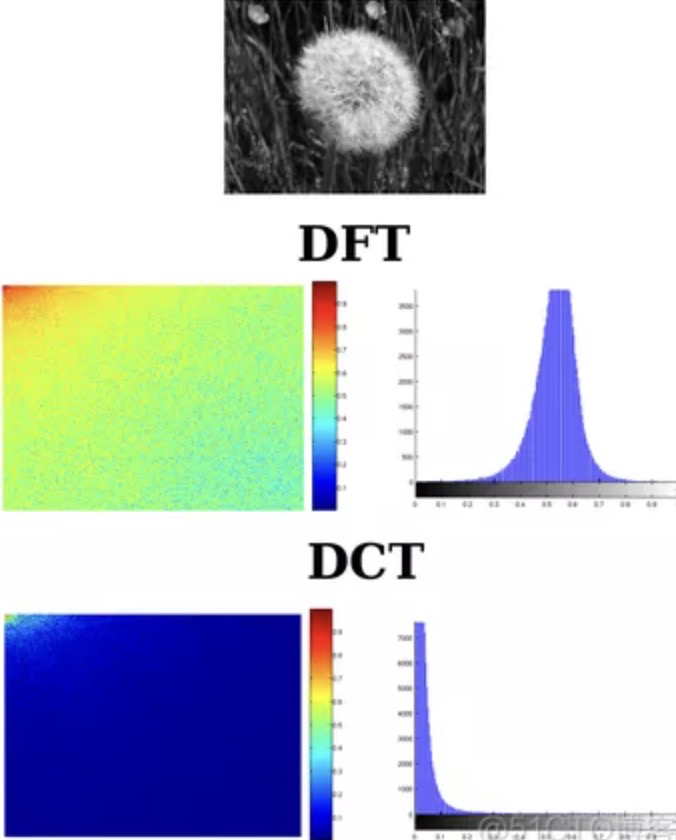
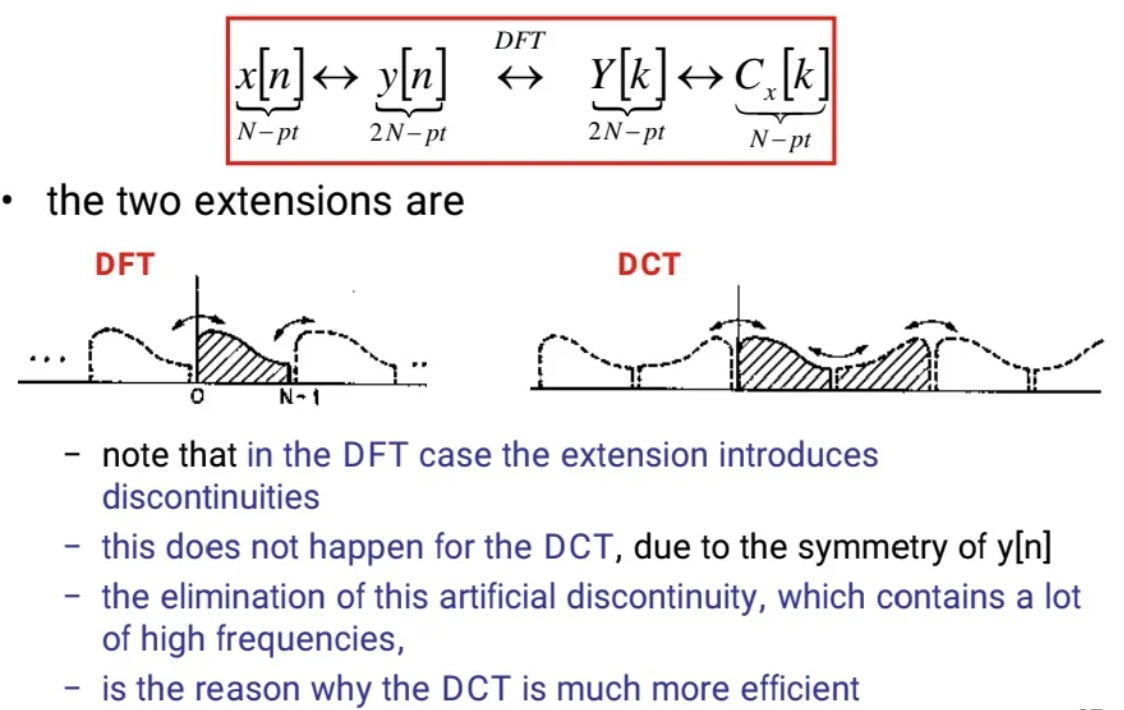
所以DCT也被认为是处理图像和语音信号的准标准变换。

简单的DCT降噪(Hard Thresh)

原始的DCT降噪非常简单，就是将图像分成小块，每个小块儿，做DCT变换，之后去除小于特点阈值的成分，然后再反变换回去即可，算法整体复杂度较低，我们这里引用OpenCV中DCT Denoise的降噪的代码进行解释。

        for (int i = range.start; i <= range.end - 1; ++i)
        {
            int y = i / (src.cols - psize);
            int x = i % (src.cols - psize);

            Rect patchNum( x, y, psize, psize );

            Mat patch(psize, psize, CV_32FC1);
            src(patchNum).copyTo( patch );

            dct(patch, patch);
            float *data = (float *) patch.data;
            for (int k = 0; k < psize*psize; ++k)
                data[k] *= fabs(data[k]) > thresh;
            idct(patch, patches[i]);
        }

Wiener Filter DCT

前面一步的结果可以给这一步做指导，用aggregate的方法来消除Ringing Artifact

Two Step DCT

执行上面两步

多尺度DCT降噪

Coast2Fine 多尺度blend

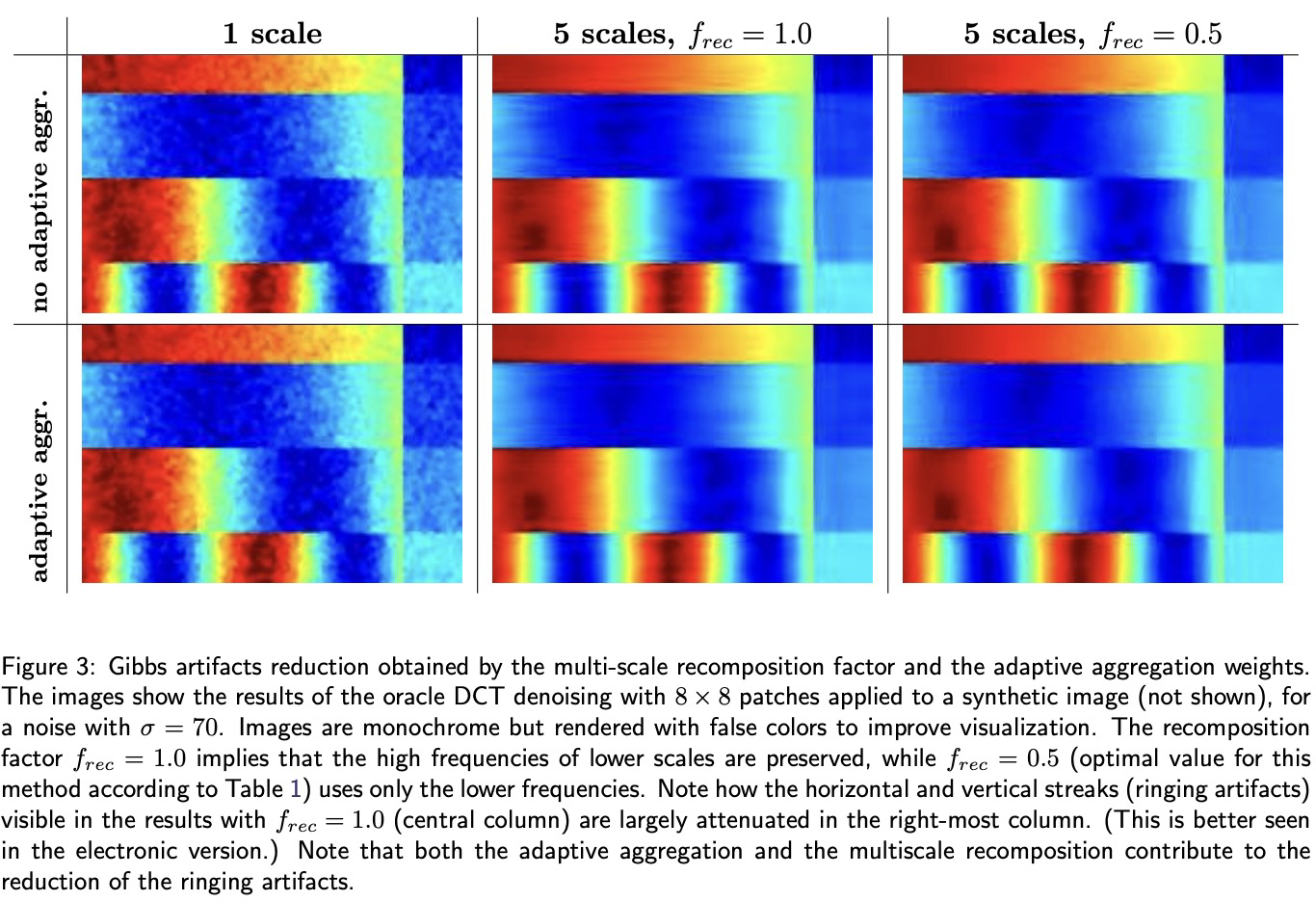
论文源码补充

需要依赖FFW3，可以先尝试下包管理工具能否直接安装，不能直接安装可以源码编译安装，下载编译地址： http://fftw.org/download.html

Mac、Linux用下面命令直接编译安装即可，Windows可以去官网找二进制包

cd fftw3
./configure
make
make install

其它package， libjpeg libpng 这些很常用，一般直接用包管理工具（homebrew、aptget、yum这些）都可以直接安装。