IEEE Float、IBM Float、VAX Float 都是常用的浮点数标准,其中IEEE745 Float 的浮点格式规范应用最广泛,这篇博客主要介绍IEEE754浮点格式规范。
参考资料
IEEE754-2019 文档:
浮点数的存储
浮点数有下面三部分构成:
- Sign 符阶,0代表正数,1代表负数
- Exp 指数,实际是Biased Exponent(有偏指数),实际使用时需要加上一个bias值
- Mantissa 尾数,科学计数法中,乘数的小数部分
计算机中常见的浮点数有float32和float64,另外也有用到float16,float80,float128,在定制化的硬件中,还可以有其它种类的浮点数表示,它们可以有不同的位阶分布,常用的float32和float64它们的存储位阶如下:
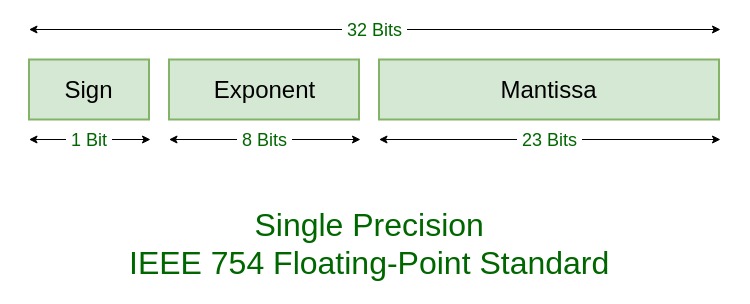
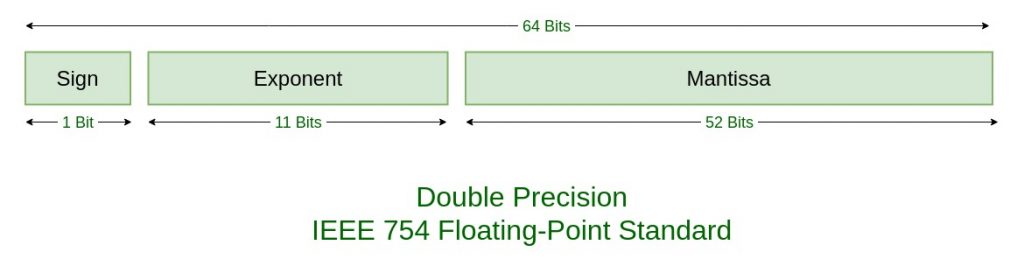
浮点数的表达
我们用下面几个记号, N 真值、S 符号,E 指数、M尾数、B指数偏置
N=(-1)^s\times2^{E-B}\times(1.M)对于32位单精度浮点数来说 B=127,E取值范围为1到254
对于64位双精度浮点数来说 B=1023,E的取值范围为1到2046
M是尾数,小数部分,因为1.X中的1是已知的,我们不会存储它
浮点数的规格化
基数为2时,尾数最高为1的数规格化。规格化时,尾数左移一位,阶码减1,尾数右移一位,阶码加1.当尾数小于等于1时,规格化就完成了。
首先将真值表示为二进制。
真值到浮点值的转换就是把真值写成下面形式
N=(-1)^s\times2^{exp}\times(1.mantissa)浮点数的基本运算
加法
a+b=(1+M_a)\times2^{E_a}+(1+M_b)\times2^{E_b} \\
\ \ \ \ = ((1+M_a)+(1+M_b)\times2^{E_b-E_a})\times2^{E_a}- 求阶差 Ea-Eb,
- 对阶,Mb*^2-(Ea-Eb),使得两数的小数点位置对齐。 对阶总是小阶向大阶看齐,阶小的数的尾数右移,右移位数等于两个阶码差的绝对值。
- 尾数求和 Ma+Mb*2^-(Ea-Eb),将对阶后的两个尾数按照定点的加减法运算规则计算。
- 规格化,增加有效数字的位数,将求和(差)后的尾数规格化 A+B = (Ma +Mb * 2^−(Ea−Eb)) * 2^a
- 舍入,为提高精度,要考虑尾数右移时候丢失的数值位
- 溢出判断,判断计算结果是否存在溢出
浮点数加法溢出
- 阶码上溢:超过了阶码可以表示的最大允许值,一般将其认为是+∞和-∞。
- 阶码下溢:超过了阶码可能表示的最小允许值,一般将其认为是0。
- 尾数上溢:两个尾数相加 / 减,最高有效位产生了进位。这种情况不一定浮点数溢出,可以尾数右移,阶码加一来重新对齐。
- 尾数下溢:在将尾数右移时,尾数的最低有效位从尾数域右端移出去,丢失了有效信息。
乘除法
a\times b=(1+M_a)\times2^{E_a}\times(1+M_b)\times2^{E_b} \\
\ \ \ \ = (1+M_a)*(1+M_b)*2^{E_a+E_b}- 阶码相加减:按照定点整数的加减法运算方法对两个浮点数的阶码进行加减运算。
- 尾数相乘或相除:按照定点小数的阵列乘除法运算方法对两个浮点数的尾数进行乘除运算。为了保证尾数相除时商的正确性,必须保证被除数尾数的绝对值一定小于除数尾数的绝对值。若被除数尾数的绝对值大于除数尾数的绝对值,需对被除数进行调整,即被除数的尾数每右移1位,阶码加1,直到被除数尾数的绝对值小于除数尾数的绝对值。
- 结果规格化并进行舍入处理:浮点数乘除运算结果的规格化和舍入处理与浮点数加减运算结果的规格化和舍入处理方法相同。并且在浮点数乘除运算的结果中,由于乘积和商的绝对值一定小于1,因此在浮点乘除运算结果进行规格化处理时只存在向左规格化,不可能出现向右规格化。
- 判断溢出:浮点数乘除运算结果的尾数不可能发生溢出,而浮点数运算结果的溢出则根据运算结果中浮点数的阶码来确定,溢出的判定和处理方法与浮点加减运算完全相同。