在描述三维场景的过程中常常用到一种名为八叉树的数据结构。描述三维空间的八叉树和描述二维空间的四叉树有相似之处,二维空间中正方形可以被分为四个相同形状的正方形,而三维空间中正方体可以被分为八个形状相同的正方体。
八叉树的每个结点表示一个正方体的体积元素,每一个结点有八个子节点,这种用于描述三维空间的树装结构叫做八叉树。为了便利的点云操作,八叉树OcTree被封装在PCL库中。
八叉树的计算原理
1. 设定最大递归深度
2. 找出场景的最大尺寸,并以此尺寸建立第一个立方体
3. 依序将单位元元素丢入能包含且没有子节点的立方体
4. 若没达到最大递归深度,就进行细分八等份,再讲该立方体所装的单位元元素全部分组给八个子立方体
5. 若发现子立方体所分配到的单位元元素数量不为零且跟父立方体一样,则该子立方体停止细分
(因为根据空间分割理论,细分的空间所得到的分配必定较少,若是一样的数目,再怎么切,数目还是一样)
6. 重复3,知道到达最大递归深度
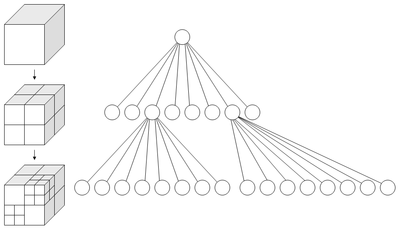
八叉树的数据结构
首先,八叉树是一种树(废话),所以可以分析它的结点,和枝干数量,这里枝干数量永远是8。假设原目标(点云)被一个大立方体包含,八叉树的作用就是细分该大立方体,每个结点对应一个立方体空间(这里类似于四叉树),八叉树的结点分为三类:
灰色结点:它对应的立方体部分被目标占据(非叶结点)
白色结点:它对应的立方体没有被目标占据(叶结点)
黑色结点:它对应的立方体完全被目标占据(叶结点)
对于非叶结点,数据结构以八元数法进行区分,分解为更小的子区块,每个区块有结点容量,当结点达到最大容量时结点停止分裂。
八叉树的存储结构
八叉树的存储结构一般分为三种:规则八叉树、线性八叉树和一对八式
规则八叉树,有九个字段,八个子叶结点,一个表征该结点灰白黑的结点,这种表示方式处于贮存空间考量,一般不使用。
线性八叉树,将八叉树转化为线性表,采用内存紧凑的方式进行表示。
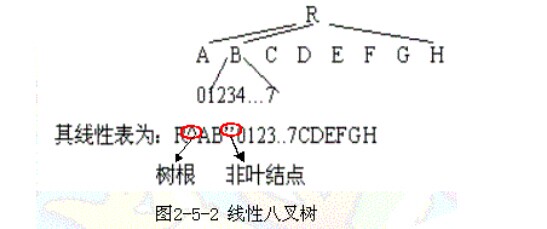
一对八表示,使用指针表示,好处是顺序可以随机
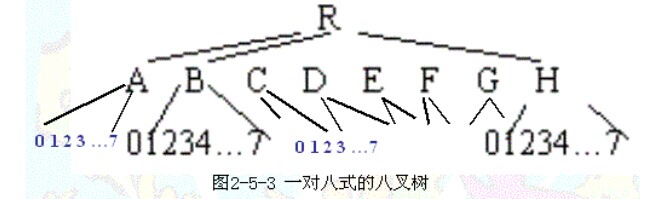
八叉树的主要优缺点
优点,使用八叉树可以快速进行三维目标的集合运算,如交、并、补、差等,亦可快速进行最邻近区域或点的搜索。
缺点,存储空间消耗。
八叉树实现
虽然PCL中封装了八叉树OcTree类,但是我们也有不得不自己写的情况,下面代买是自己摘抄的(自己当然还是用PCL了)
#include <iostream>
using namespace std;
//定义八叉树节点类
template<class T>
struct OctreeNode
{
T data; //节点数据
T xmin,xmax; //节点坐标,即六面体个顶点的坐标
T ymin,ymax;
T zmin,zmax;
OctreeNode <T>*top_left_front,*top_left_back; //该节点的个子结点
OctreeNode <T>*top_right_front,*top_right_back;
OctreeNode <T>*bottom_left_front,*bottom_left_back;
OctreeNode <T>*bottom_right_front,*bottom_right_back;
OctreeNode //节点类
(T nodeValue = T(),
T xminValue = T(),T xmaxValue = T(),
T yminValue = T(),T ymaxValue = T(),
T zminValue = T(),T zmaxValue = T(),
OctreeNode<T>*top_left_front_Node = NULL,
OctreeNode<T>*top_left_back_Node = NULL,
OctreeNode<T>*top_right_front_Node = NULL,
OctreeNode<T>*top_right_back_Node = NULL,
OctreeNode<T>*bottom_left_front_Node = NULL,
OctreeNode<T>*bottom_left_back_Node = NULL,
OctreeNode<T>*bottom_right_front_Node = NULL,
OctreeNode<T>*bottom_right_back_Node = NULL )
:data(nodeValue),
xmin(xminValue),xmax(xmaxValue),
ymin(yminValue),ymax(ymaxValue),
zmin(zminValue),zmax(zmaxValue),
top_left_front(top_left_front_Node),
top_left_back(top_left_back_Node),
top_right_front(top_right_front_Node),
top_right_back(top_right_back_Node),
bottom_left_front(bottom_left_front_Node),
bottom_left_back(bottom_left_back_Node),
bottom_right_front(bottom_right_front_Node),
bottom_right_back(bottom_right_back_Node){}
};
//创建八叉树
template <class T>
void createOctree(OctreeNode<T> * &root,int maxdepth,double xmin,double xmax,double ymin,double ymax,double zmin,double zmax)
{
//cout<<"处理中,请稍候……"<<endl;
maxdepth=maxdepth-1; //每递归一次就将最大递归深度-1
if(maxdepth>=0)
{
root=new OctreeNode<T>();
cout<<"请输入节点值:";
//root->data =9;//为节点赋值,可以存储节点信息,如物体可见性。由于是简单实现八叉树功能,简单赋值为9。
cin>>root->data; //为节点赋值
root->xmin=xmin; //为节点坐标赋值
root->xmax=xmax;
root->ymin=ymin;
root->ymax=ymax;
root->zmin=zmin;
root->zmax=zmax;
double xm=(xmax-xmin)/2;//计算节点个维度上的半边长
double ym=(ymax-ymin)/2;
double zm=(ymax-ymin)/2;
//递归创建子树,根据每一个节点所处(是几号节点)的位置决定其子结点的坐标。
createOctree(root->top_left_front,maxdepth,xmin,xmax-xm,ymax-ym,ymax,zmax-zm,zmax);
createOctree(root->top_left_back,maxdepth,xmin,xmax-xm,ymin,ymax-ym,zmax-zm,zmax);
createOctree(root->top_right_front,maxdepth,xmax-xm,xmax,ymax-ym,ymax,zmax-zm,zmax);
createOctree(root->top_right_back,maxdepth,xmax-xm,xmax,ymin,ymax-ym,zmax-zm,zmax);
createOctree(root->bottom_left_front,maxdepth,xmin,xmax-xm,ymax-ym,ymax,zmin,zmax-zm);
createOctree(root->bottom_left_back,maxdepth,xmin,xmax-xm,ymin,ymax-ym,zmin,zmax-zm);
createOctree(root->bottom_right_front,maxdepth,xmax-xm,xmax,ymax-ym,ymax,zmin,zmax-zm);
createOctree(root->bottom_right_back,maxdepth,xmax-xm,xmax,ymin,ymax-ym,zmin,zmax-zm);
}
}
int i=1;
//先序遍历八叉树
template <class T>
void preOrder( OctreeNode<T> * & p)
{
if(p)
{
cout<<i<<".当前节点的值为:"<<p->data<<"\n坐标为:";
cout<<"xmin: "<<p->xmin<<" xmax: "<<p->xmax;
cout<<"ymin: "<<p->ymin<<" ymax: "<<p->ymax;
cout<<"zmin: "<<p->zmin<<" zmax: "<<p->zmax;
i+=1;
cout<<endl;
preOrder(p->top_left_front);
preOrder(p->top_left_back);
preOrder(p->top_right_front);
preOrder(p->top_right_back);
preOrder(p->bottom_left_front);
preOrder(p->bottom_left_back);
preOrder(p->bottom_right_front);
preOrder(p->bottom_right_back);
cout<<endl;
}
}
//求八叉树的深度
template<class T>
int depth(OctreeNode<T> *& p)
{
if(p == NULL)
return -1;
int h =depth(p->top_left_front);
return h+1;
}
//计算单位长度,为查找点做准备
int cal(int num)
{
int result=1;
if(1==num)
result=1;
else
{
for(int i=1;i<num;i++)
result=2*result;
}
return result;
}
//查找点
int maxdepth=0;
int times=0;
static double xmin=0,xmax=0,ymin=0,ymax=0,zmin=0,zmax=0;
int tmaxdepth=0;
double txm=1,tym=1,tzm=1;
template<class T>
void find(OctreeNode<T> *& p,double x,double y,double z)
{
double xm=(p->xmax-p->xmin)/2;
double ym=(p->ymax-p->ymin)/2;
double zm=(p->ymax-p->ymin)/2;
times++;
if(x>xmax || x<xmin|| y>ymax || y<ymin || z>zmax || z<zmin)
{
cout<<"该点不在场景中!"<<endl;
return;
}
if(x<=p->xmin+txm&& x>=p->xmax-txm && y<=p->ymin+tym &&y>=p->ymax-tym && z<=p->zmin+tzm &&z>=p->zmax-tzm )
{
cout<<endl<<"找到该点!"<<"该点位于"<<endl;
cout<<"xmin: "<<p->xmin<<" xmax: "<<p->xmax;
cout<<"ymin: "<<p->ymin<<" ymax: "<<p->ymax;
cout<<"zmin: "<<p->zmin<<" zmax: "<<p->zmax;
cout<<"节点内!"<<endl;
cout<<"共经过"<<times<<"次递归!"<<endl;
}
else if(x<(p->xmax-xm) && y<(p->ymax-ym) &&z<(p->zmax-zm))
{
cout<<"当前经过节点坐标:"<<endl;
cout<<"xmin: "<<p->xmin<<" xmax: "<<p->xmax;
cout<<"ymin: "<<p->ymin<<" ymax: "<<p->ymax;
cout<<"zmin: "<<p->zmin<<" zmax: "<<p->zmax;
cout<<endl;
find(p->bottom_left_back,x,y,z);
}
else if(x<(p->xmax-xm) && y<(p->ymax-ym) &&z>(p->zmax-zm))
{
cout<<"当前经过节点坐标:"<<endl;
cout<<"xmin: "<<p->xmin<<" xmax: "<<p->xmax;
cout<<"ymin: "<<p->ymin<<" ymax: "<<p->ymax;
cout<<"zmin: "<<p->zmin<<" zmax: "<<p->zmax;
cout<<endl;
find(p->top_left_back,x,y,z);
}
else if(x>(p->xmax-xm) && y<(p->ymax-ym) &&z<(p->zmax-zm))
{
cout<<"当前经过节点坐标:"<<endl;
cout<<"xmin: "<<p->xmin<<" xmax: "<<p->xmax;
cout<<"ymin: "<<p->ymin<<" ymax: "<<p->ymax;
cout<<"zmin: "<<p->zmin<<" zmax: "<<p->zmax;
cout<<endl;
find(p->bottom_right_back,x,y,z);
}
else if(x>(p->xmax-xm) && y<(p->ymax-ym) &&z>(p->zmax-zm))
{
cout<<"当前经过节点坐标:"<<endl;
cout<<"xmin: "<<p->xmin<<" xmax: "<<p->xmax;
cout<<"ymin: "<<p->ymin<<" ymax: "<<p->ymax;
cout<<"zmin: "<<p->zmin<<" zmax: "<<p->zmax;
cout<<endl;
find(p->top_right_back,x,y,z);
}
else if(x<(p->xmax-xm) && y>(p->ymax-ym) &&z<(p->zmax-zm))
{
cout<<"当前经过节点坐标:"<<endl;
cout<<"xmin: "<<p->xmin<<" xmax: "<<p->xmax;
cout<<"ymin: "<<p->ymin<<" ymax: "<<p->ymax;
cout<<"zmin: "<<p->zmin<<" zmax: "<<p->zmax;
cout<<endl;
find(p->bottom_left_front,x,y,z);
}
else if(x<(p->xmax-xm) && y>(p->ymax-ym) &&z>(p->zmax-zm))
{
cout<<"当前经过节点坐标:"<<endl;
cout<<"xmin: "<<p->xmin<<" xmax: "<<p->xmax;
cout<<"ymin: "<<p->ymin<<" ymax: "<<p->ymax;
cout<<"zmin: "<<p->zmin<<" zmax: "<<p->zmax;
cout<<endl;
find(p->top_left_front,x,y,z);
}
else if(x>(p->xmax-xm) && y>(p->ymax-ym) &&z<(p->zmax-zm))
{
cout<<"当前经过节点坐标:"<<endl;
cout<<"xmin: "<<p->xmin<<" xmax: "<<p->xmax;
cout<<"ymin: "<<p->ymin<<" ymax: "<<p->ymax;
cout<<"zmin: "<<p->zmin<<" zmax: "<<p->zmax;
cout<<endl;
find(p->bottom_right_front,x,y,z);
}
else if(x>(p->xmax-xm) && y>(p->ymax-ym) &&z>(p->zmax-zm))
{
cout<<"当前经过节点坐标:"<<endl;
cout<<"xmin: "<<p->xmin<<" xmax: "<<p->xmax;
cout<<"ymin: "<<p->ymin<<" ymax: "<<p->ymax;
cout<<"zmin: "<<p->zmin<<" zmax: "<<p->zmax;
cout<<endl;
find(p->top_right_front,x,y,z);
}
}
//main函数
int main ()
{
OctreeNode<double> *rootNode = NULL;
int choiced = 0;
while(true)
{
system("cls");
cout<<"请选择操作:\n";
cout<<"1.创建八叉树 2.先序遍历八叉树\n";
cout<<"3.查看树深度 4.查找节点 \n";
cout<<"0.退出\n\n";
cin>>choiced;
if(choiced == 0)
return 0;
else if(choiced == 1)
{
system("cls");
cout<<"请输入最大递归深度:"<<endl;
cin>>maxdepth;
cout<<"请输入外包盒坐标,顺序如下:xmin,xmax,ymin,ymax,zmin,zmax"<<endl;
cin>>xmin>>xmax>>ymin>>ymax>>zmin>>zmax;
if(maxdepth>=0|| xmax>xmin || ymax>ymin || zmax>zmin || xmin>0 || ymin>0||zmin>0)
{
tmaxdepth=cal(maxdepth);
txm=(xmax-xmin)/tmaxdepth;
tym=(ymax-ymin)/tmaxdepth;
tzm=(zmax-zmin)/tmaxdepth;
createOctree(rootNode,maxdepth,xmin,xmax,ymin,ymax,zmin,zmax);
}
else
{
cout<<"输入错误!";
return 0;
}
}
else if(choiced == 2)
{
system("cls");
cout<<"先序遍历八叉树结果:/n";
i=1;
preOrder(rootNode);
cout<<endl;
system("pause");
}
else if(choiced == 3)
{
system("cls");
int dep =depth(rootNode);
cout<<"此八叉树的深度为"<<dep+1<<endl;
system("pause");
}
else if(choiced == 4)
{
system("cls");
cout<<"请输入您希望查找的点的坐标,顺序如下:x,y,z\n";
double x,y,z;
cin>>x>>y>>z;
times=0;
cout<<endl<<"开始搜寻该点……"<<endl;
find(rootNode,x,y,z);
system("pause");
}
else
{
system("cls");
cout<<"\n\n错误选择!\n";
system("pause");
}
}
}
您好,博主:
我在github上看到您分享的RVAF代码,有一些问题想向你学习一下,一直没找到您的邮箱,所以在这里留言了。
首先非常感谢您的分享,最近我也在应用ACF算法做一些检测,仔细看了您的算法,对我帮助很大。在算法中有一个色彩空间转换表bgr2luv.dat文件,不知您能否分享一下?
非常感谢。不知可否留下您的联系方式,方便以后跟您请教。
祝您工作愉快
晚上回去更新GitHub,应该十一点前可以看到
好的,我随时关注着,感谢博主的回复,刚刚我在代码注释中找到了您的邮箱me@p-chao.com,不知以后有问题可否通过这个邮箱向您请教?
deeplearning@vip.qq.com
那个邮箱垃圾邮件太多,已经不用了