上一篇博客我们完成了一个六行的SVM,对python中数据和估计器等概念有了认识,这篇博客将更加详细的对sklearn的训练进行解释,同时也按照官网例程运行KNN和SVM等具有代表性的demo。
这节笔记对应的官网教程为: Statistical learning: the setting and the estimator object in scikit-learn 和 Supervised learning: predicting an output variable from high-dimensional observations
数据集
上一节已经介绍过,这一节我们加载的是 安德森鸢尾花卉数据集 :
>>> from sklearn import datasets >>> iris = datasets.load_iris() >>> data = iris.data >>> data.shape (150, 4)
估计器
在回顾一下上一节我们用过的SVM估计器,fit(x,y)来进行训练,predict(x)来进行预测,每个估计器都有着两个方法,估计器还可以输入很多参数:
>>> estimator.fit(data) >>> estimator = Estimator(param1=1, param2=2) >>> estimator.param1 1
还可以通过如下方式直接获取估计器最终的全部参数
>>> estimator.estimated_param_
KNN分类
首先我们加载数据,np.unique(y) 保留对象中不重复的元素,这样我们就可以获取不重复的类别标签,我们可以看到我们需要分类的数据共有三类:
>>> import numpy as np >>> from sklearn import datasets >>> iris = datasets.load_iris() >>> iris_X = iris.data >>> iris_y = iris.target >>> np.unique(iris_y) array([0, 1, 2])
然后我们选取最后十个为测试集,前面的为训练集,使用KNN进行分类。
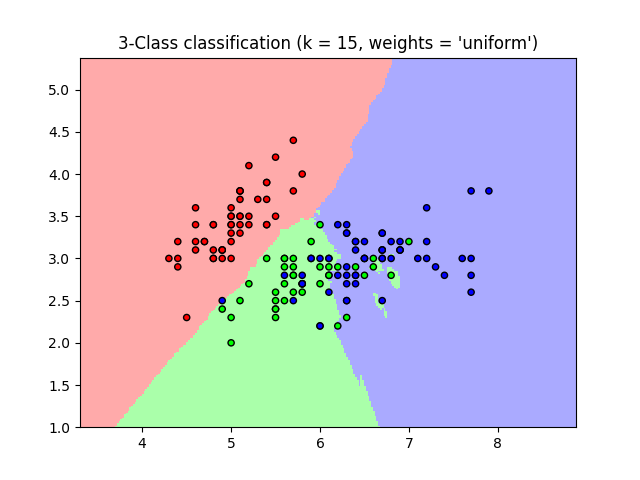
>>> # Split iris data in train and test data
>>> # A random permutation, to split the data randomly
>>> np.random.seed(0)
>>> indices = np.random.permutation(len(iris_X))
>>> iris_X_train = iris_X[indices[:-10]]
>>> iris_y_train = iris_y[indices[:-10]]
>>> iris_X_test = iris_X[indices[-10:]]
>>> iris_y_test = iris_y[indices[-10:]]
>>> # Create and fit a nearest-neighbor classifier
>>> from sklearn.neighbors import KNeighborsClassifier
>>> knn = KNeighborsClassifier()
>>> knn.fit(iris_X_train, iris_y_train)
KNeighborsClassifier(algorithm='auto', leaf_size=30, metric='minkowski',
metric_params=None, n_jobs=1, n_neighbors=5, p=2,
weights='uniform')
>>> knn.predict(iris_X_test)
array([1, 2, 1, 0, 0, 0, 2, 1, 2, 0])
>>> iris_y_test
array([1, 1, 1, 0, 0, 0, 2, 1, 2, 0])
np.random.seed(0)的作用是为后面的随机算法设置种子,这里设置0使每次运行程序生成的随机数相同,相同的seed生成相同的随机数,不涉及seed每次回生成不同的随机数。
np.random.permutation(150)则返回0-149共150长度向量的洗牌,后面将其作为下标,用来打乱数据。
后面代码简单运用了KNN,就不多解释了,如果不懂可以看之前的教程。
维度灾难
维度灾难是指,当特征数量逐步增加到一定规模后,分类器性能是下降的。在低维度空间中,我们很容易找到分类平面,而当特征规模达到一定程度后,我们需要更多数据才能确定分类超平面。在官网教程中举了KNN的例子,维度增加对应的需求数据增加是指数量级的。在分类中我们使用的特征数量越多,那么由于高维下数据的稀疏性我们不得不需要更多数据来对分类器的参数进行估计。除此之外还有另一个影响,就是数据的稀疏性致使数据的分布在空间上是不同的。
线性回归
我们将从线性回归开始,逐步引入稀疏的概念,这该过程中我们处理高维数据。线性回归模型表示如下,我们的目标是使模型误差的平方和最小[mathjax]
$$y=X\beta+\epsilon$$
- $latex X$:数据
- $latex y$:目标变量
- $latex \beta$:回归参数
- $latex \epsilon$:观测噪声

下面是实现的代码,前面五行加载了diabetes数据集,这也是一个很有名的数据集,包含442个样本的(age,sex,weight,blood pressure…)等十个参数,然后来预测一年之后的参数,是一个典型的回归问题。下面的代码先用线性回归来拟合参数,然后输出了拟合得到的模型参数regr.coef_,然后计算了均方误差,输出了评价分数:
>>> diabetes = datasets.load_diabetes() >>> diabetes_X_train = diabetes.data[:-20] >>> diabetes_X_test = diabetes.data[-20:] >>> diabetes_y_train = diabetes.target[:-20] >>> diabetes_y_test = diabetes.target[-20:] >>> from sklearn import linear_model >>> regr = linear_model.LinearRegression() >>> regr.fit(diabetes_X_train, diabetes_y_train) LinearRegression(copy_X=True, fit_intercept=True, n_jobs=1, normalize=False) >>> print(regr.coef_) [ 0.30349955 -237.63931533 510.53060544 327.73698041 -814.13170937 492.81458798 102.84845219 184.60648906 743.51961675 76.09517222] >>> # The mean square error >>> np.mean((regr.predict(diabetes_X_test)-diabetes_y_test)**2) 2004.56760268... >>> # Explained variance score: 1 is perfect prediction >>> # and 0 means that there is no linear relationship >>> # between X and y. >>> regr.score(diabetes_X_test, diabetes_y_test) 0.5850753022690...
数据缩减
如果每个维度数据更少,那么噪声将造成更大影响。我们来看下面这段代码:
>>> from sklearn import linear_model >>> X = np.c_[ .5, 1].T >>> y = [.5, 1] >>> test = np.c_[ 0, 2].T >>> regr = linear_model.LinearRegression() >>> import matplotlib.pyplot as plt >>> plt.figure() >>> np.random.seed(0) >>> for _ in range(6): ... this_X = .1*np.random.normal(size=(2, 1)) + X ... regr.fit(this_X, y) ... plt.plot(test, regr.predict(test)) ... plt.scatter(this_X, y, s=3)
上面这段代码运行之后,窗口绘制的图形是这个样子的:

稀疏