在三维空间中,角向自由度常常用欧拉角表示,就是说欧拉角是形容两个坐标空间旋转关系的,所以思考问题时需要一定的立体感,而在欧拉角计算过程中,有常常涉及到一些关系计算和数学转换。
这篇博客摘录了即几篇优质博客的内容,涉及欧拉角、旋转矩阵、旋转向量、欧拉角换算等诸多问题。
一、欧拉角
[mathjax]
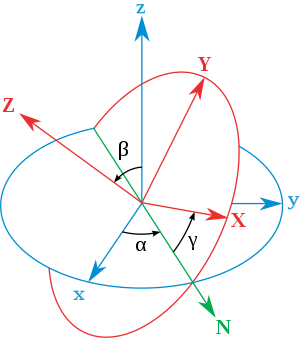
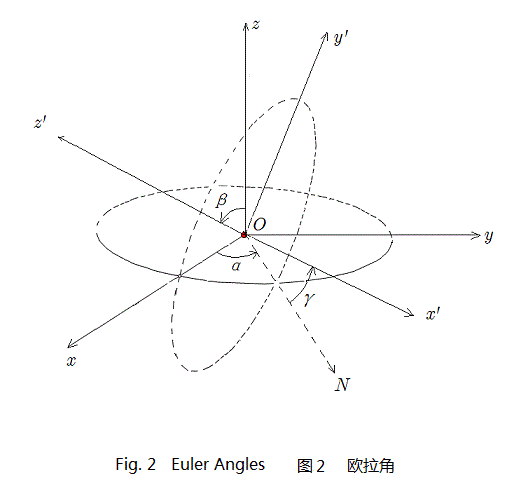
先上两个图,说说欧拉角是怎么来的?我们注意上面右图,定义欧拉角需要借助一条辅助线N,这条辅助线就是交规线,为旋转前后坐标系XY平面间的夹角,其实N也就是x轴绕着z轴旋转$latex \alpha$。我们一般会把两个XY平面用圆弧表示出来。于是欧拉角定义如下:
- $latex \alpha$ 为x轴与N轴的角度
- $latex \beta$ 为z轴与Z轴的角度
- $latex \gama$ 为N轴与x轴的角度
根据下面这幅动图,来理解欧拉角,$latex \alpha$就是绕着Z旋转的角度,然后绕着新的x轴,也就是N旋转,然后再绕着新的Z轴旋转,这样我们就完成了一次坐标系旋转。

二、欧拉角与旋转矩阵
绕着各个坐标轴分别旋转的旋转矩阵为

然后得到整体的旋转矩阵
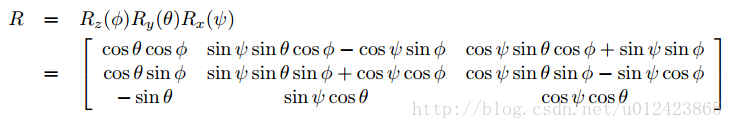
三、通过旋转矩阵计算欧拉角
如果一个旋转矩阵为

那么它对应的欧拉角为
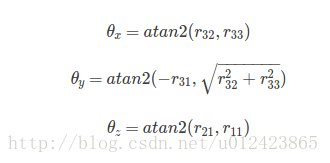
四、欧拉角与旋转向量
参见谢国芳公式:
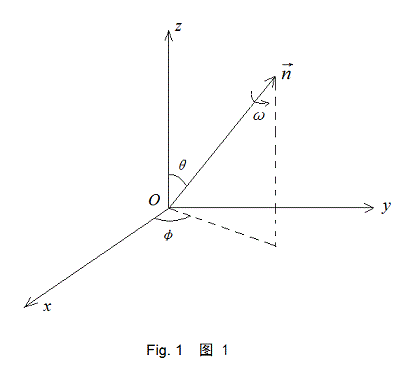

五、旋转矩阵与旋转向量
参见我之前的博客,Rodrigues变换(含代码)
提醒下,推测欧拉角的旋转向量,也可以通过旋转矩阵进行中间转化。
注意:你的图像用的是ZXZ系统而R旋转矩阵用ZYZ系统。
是的,多谢提点,文字表述用的ZXZ,粘的图对不上
已知欧拉角如何反推图1的β角,也就是两个平面的夹角。