列维-奇维塔符号(Levi-Civita symbol)和 爱因斯坦标记(Einstein notation)是张量运算的常用标记。
爱因斯坦求和约定(Einstein summation convention)又称为爱因斯坦标记法(Einstein notation),可以让表达式更加简洁明了。里面主要涉及两个概念:哑标(dummy index),自由标(free index)
定义
哑标:在表达式的某项中,若某下标重复出现两次,则表示要把该项指标在取值范围内遍历求和,该重复指标称为哑标,未被求和的下标被称为自由标
自由标:在表达式某项中,若某下标只出现一次,若在取值范围内轮流取该下表的任意值时,关系式恒成立,则该下标被称为自由标。
哑标只能成对出现,头则要加上特别符号说明
若重复标号不求和,应特别声明
einsum表达式
我们先看下面一个矩阵乘法的表达式
np.einsum(‘ij,jk->ik’, A, B)
我们把’->’看作输入和输出的分隔符,左侧两个输入用’, ‘ 隔开,熟悉线形代数的话,就很容易从下标理解操作了:
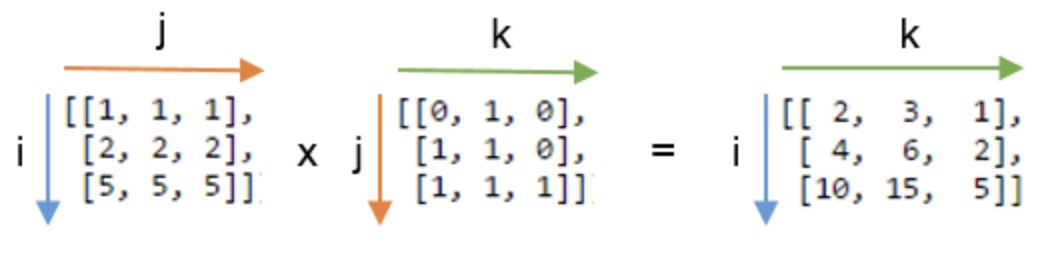
回顾我们前面提到的概念,’ij,jk’ 中 j 重复用了两次, 1次表示A的第二个轴,1ci表示B的第一个轴,要保证输入合法,意味着A的第二个轴和B的第一个轴做乘积,就需要A行长和B列长一致。
如果某个轴标签在输出标签消失了,则表示要沿着该轴做求和运算。同时我们也可以获取任意轴序的结果输出。了解基本规则之后,我们可以理解einsum是非常节约空间的计算函数,einsum不构建中间临时的array,直接累加的到最终结果。
einsum操作
如果A和B是1D array,A和B的形状总是合适的
| Call signature | NumPy equivalent | Description |
|---|---|---|
| (‘i’, A) | A | A |
| (‘i->’, A) | sum(A) | A的所有元素和 |
| (‘i,i->i’, A, B) | A * B | A和B逐元素乘积 |
| (‘i,i’, A, B) | inner(A, B) | A和B的内积 |
| (‘i,j->ij’, A, B) | outer(A, B) | A和B的外积 |
如果A和B是两个2D arrays, 假设在相应操作中,A和B的形状是合适的,那么:
| Call signature | NumPy equivalent | Description |
|---|---|---|
| (‘ij’, A) | A | A |
| (‘ji’, A) | A.T | A的转置 |
| (‘ii->i’, A) | diag(A) | A 的对角 |
| (‘ii’, A) | trace(A) | A的迹 |
| (‘ij->’, A) | sum(A) | A的所有元素和 |
| (‘ij->j’, A) | sum(A, axis=0) | A的沿着axis=0的和 |
| (‘ij->i’, A) | sum(A, axis=1) | A的沿着axis=1的和 |
| (‘ij,ij->ij’, A, B) | A * B | A和B逐元素乘积 |
| (‘ij,ji->ij’, A, B) | A * B.T | A 和 B.T 逐元素乘积 |
| (‘ij,jk’, A, B) | dot(A, B) | A 和 B 的矩阵乘法 |
| (‘ij,kj->ik’, A, B) | inner(A, B) | A 和 B 的内积 |
| (‘ij,kj->ikj’, A, B) | A[:, None] * B | A的每一行与B的乘积 |
| (‘ij,kl->ijkl’, A, B) | A[:, :, None, None] * B | A的每一个元素与B的乘积 |
‘->’ 符号省略时,一般时看作A末尾下表和B前面下标相同,进行的省略
einsum中的 ‘…’ 符号,在处理比较多维度时,可以像numpy array 一样使用 ‘…’ 符号省略一些维度的显式表示。例如:
np.einsum(‘…ij,ji->…’, a, b)
注意,einsum求和时,不会提升数据类型,因此处理尾款比较小的数据可能得不到预期的结果
einsum在numpy计算库中并不一定总是最快的,dot和inner 函数一般使用快速计算库blas,计算速度更快一些。
参考链接:https://blog.popkx.com/A-basic-introduction-to-NumPy-s-einsum/