上一篇博客 简单介绍了期权的四个交易方向,大致梳理了期权交易策略,期权实际操作中面临着多种风险,我们可以根据这些风险的特点来制定交易策略,这篇博客详细介绍期权的风险评价指标,就是著名的五个希腊字母 Delta(方向)、Gamma、Vega(波动率)、Theta(时间)、Rho(利率)。
期权的风险来源
Delta来自于标的物本身、Gamma来自于Delta的变动、Vega是有关波动率风险的指标、Theta是和到期时间相关的风险、Rho为利率风险
| 指标参数 | 风险来源 | 价值公式 |
| Delta | 标的物价格变化 | 权利金变动/标的物价格的变动 |
| Gamma | Delta的变动 | Delta的变动/标的物价格的变动 |
| Vega | 标的物价格波动率的变动 | 权利金的变动/波动率的变动 |
| Theta | 距到期日的变动 | 权利金的变动/到期日的变动 |
| Rho | 投资于标的物资金的利息率的变动 | 权利金的变动/利息的变动 |
一、Delta
1. Delta值概述
Delta值又称作对冲值,是衡量标的资产价格变动时,期权价格的变化幅度。
公式表示:
\Delta=\frac{期权价格变化}{标的价格变化}一般标的的期权又很多行权价,相对于标的物价格上涨,不同行权价的权利金变化浮动通常不同。期权价格变动相对于标的价格的变动率,就用Delta来描述。
2. Delta值特性
风险指标的正负号均是从买入期权的角度来考虑的。
Call的Delta一定要是正值,Put的Delta一定是负值,数值范围为0到1。如果标的上涨,Call的权利金上涨,Delta为正,Put的Delta为负。
平值看涨期权Delta为0.5,虚值看涨期权的delta则逼近于0。
| Options | 虚值状态 Delta | 平值状态 Delta | 实值状态 Delt |
| Buy Call | 0-0.5 | 0.5 | 0.5-1 |
| Sell Put | 0-0.5 | 0.5 | 0.5-1 |
| Buy Put | -0.5-0 | -0.5 | -1-(-0.5) |
| Sell Call | -0.5-0 | -0.5 | -1-(-0.5) |
虚值期权Delta为0,意味着证券到期时,期权持有者一定不会获得收益,期权价格也就不随着标的价格变动而变动。
实值期权Delta为1,意味着证券到期时,期权持有者一定会获得收益,期权价格完全跟随标的价格变动而变动。
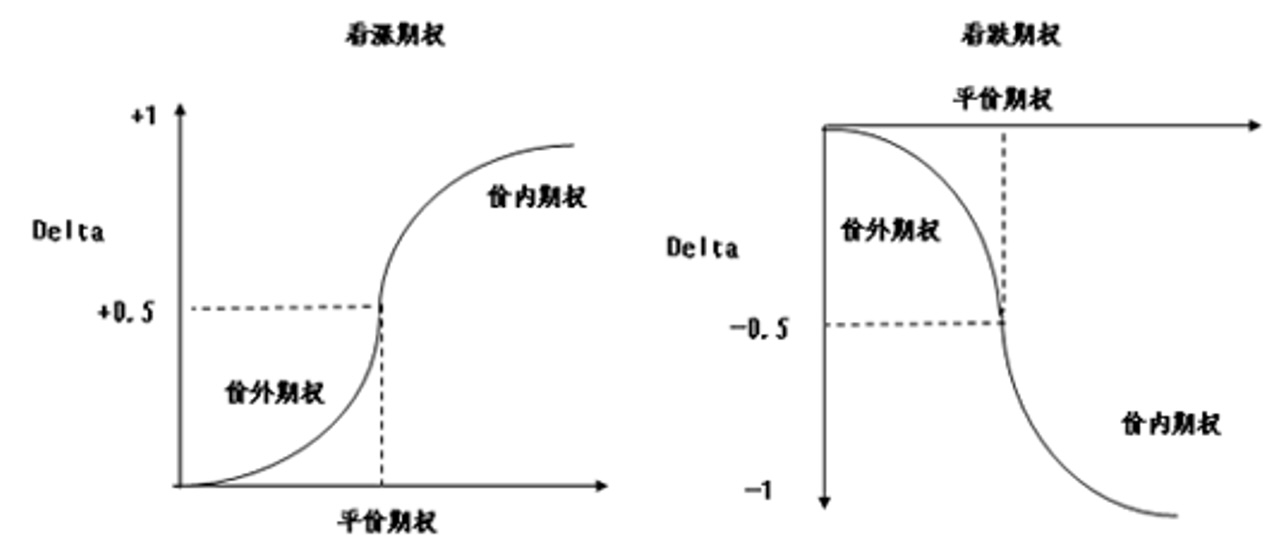
另外,Delta值并不是一个静态概念,让随着到期时间、期权价格水平不同而随时发生变化。也就意味着,只有标的价格发生微小变化时,Delta预测的结果才是有效的。
投资组合的Delta数值可以直接相加。假设投资组合两个期权的Delta数值分别为0.5和0.3,整个组合的Delta数值将会是0.8.
3. Delta值的应用
衡量部位风险
我们拿下列投资组合举个例子:
| 持仓部位 | Delta | 数量 |
| 买入标的 | 1 | 1 |
| 买入看涨期权 | 0.47 | 2 |
| 买入看跌期权 | -0.53 | 3 |
我们可以将上述组合所有部位的Delta值相加:
1+2×0.47-3×0.53=0.35
可见,该交易组合的总体持仓Delta值为0.35,也就是说这是一个偏多的部位,想到于0.35手多头标的。
Delta Hedgin (Delta中性套期保值)
如果投资者希望对冲期权或标的部位的风险,Delta就是套期保值比率。只要使部位整体Delta保持围0,就建立了一个Delta Hedgin策略。
例如,投资者持有10手看跌期权,每手看跌期权的Delta值为-0.2,部位的Delta为-2。投资者可以通过其它交易使Delta值归0,来实现组合Delta的中性,规避10手看跌期权多头的风险。
Delta是静态的,只在标的价格变化不大时有效,如果标的大幅变化,Delta本身也会变化,仅仅依靠Delta做预测就会失效,那么我们就需要引入下一个参数了。
二、Gamma
1. Gamma值概述
Gamma反映标的价格对Delta值的影响程度。为delta变化量与标的价格变化量之比。
如某一期权的Delta为0.6, gamma值为0.05,则表示期货价格上升1元,所引起delta增加量为0.05,delta将从0.6增加到0.65。
\gamma=\frac{\Delta 的变化}{标的价格的变化}2. Gamma值特性
与Delta不同,不论Call还是Put,Buy的gamma均为正值,Sell的gamma值均为负值。
标的价格上涨,Call的Delta由0向1移动,Put的Delta从-1向0移动,gamma值为正。
标的价格下跌,Call的Delta由1向0移动,Put的Delta从0向-1移动,gamma值为正。
平值期权Gamma值大于实值、虚值期权
深度实值和深度虚值期权的Gamma趋近于0, 随着到期日临近,平值期权的Gamma值会急剧增加。
当价格波动率上升,实值或虚值期权Gamma值降增加,平值期权的Gamma值减少。
Gamma的绝对值越大,权利金变化越快。Gamma的绝对值越小,权利金变化越慢。
3. Gamma值应用
价外期权变为平价时,其Gamma值达到最高。平价期权回落至价外,权证的跌幅也会较大。
持仓头寸控制
Gamma的风险可以从它取值大小来看。当Gamma的绝对值很小时,投资者进行的Delta中性交易不需要调整太频繁,但是如果Gamma的绝对值很大时,表明Delta的变化速度非常快。
此时,是假对期权价格的作用更强,Delta中性交易组合策略需要及时调整,否则会存在很大风险。
初学期权交易的人往往被告诫避免大的Gamma组合,尤其是负的Gamma。应当通过Delta和Gamma,将风险控制在可承受范围。
Gamma也有助于保持Delta中性,比如某交易者有+6Delta部位,卖出6个期货合约,加入Gamma为+1,市场上涨2个点,此时Delta就变为+8,为了达到Delta中性,该交易者就必须再卖出2个期货。
三、Theta
1. Theta值概述
期权价格包含内在价值和时间价值,我们常说时间是期权买方的敌人、卖方的朋友,我们也可以从Theta来理解这句话。
Theta值是用来测量时间变化对期权理论价值的影响。表示时间经过一天,期权价值会损失多少。
\Theta=\frac{期权价格的变化}{距离到期日时间的变化}2.Theta值特点
Theta的数值通常为负数,其绝对值会随着时间消逝而变大,最后到期时权证的时间价值应等于0。
平值期权的Theta绝对值大于实值、虚值期权。
短期期权的价值损耗快于长期期权。
价格波动率上升,期权的Theta绝对值将上升。
3. Theta值应用
Theta常常可以想象为燃料测量工具。它计量期权还有多长时间并在什么时间耗尽“燃料”。
下图中的Theta价值包括平价、盈价、亏价看涨期权的价值。Theta告诉我们在距离到期日较远时,随着时间过去一天,非平价期权具有时间衰减线形比率,一个理由是期权时间价值相当小,时间衰减与交易策略产生的影响相比,前一想影响是重要的。

四、Vega
1. Vega值概述
在权利金的影响因素中,最不确定是波动率。
当隐含波动率涨跌时,期权价格也随之涨跌,Vega就是衡量标的物价格升跌1%对权利金的影响。公式表示为:
v=\frac{期权价格变化}{波动率的变化}2. Vega值特点
在其它因素不变的前提下,波动率越高,期权理论价值越高。期权多头Vega都是正数,期权空头Vega是负数。
隐含波动率上升会使得期权价格上涨,这对多头有利。买入看涨或看跌,Vega值都是正数,而卖出方向对应的Vega值则为负数。
随着时间的流逝,任何期权的Vega值都会下降。
因为平值期权的时间价值最高,所以具有最大的Vega值,而深实值、深虚值期权的Vega接近0,平值期权的Vega值对于波动率变化不太敏感,保持相对稳定,但在临近到期,当平值期权价值以非线形速度衰减时,Vega值也以类似的方式衰减。
我们重新梳理一下多头和空头的Gamma、Theta、Vega的符号,来看哪些因素对买卖方有利
| 多头(Long) | +Gamma | -Theta | +Vega |
| 空头(Short) | -Gamma | +Theta | -Vega |
3. Vega值应用
如果投资组合Vega值是正数,将会从价格波动率的上涨中获利,反之则希望价格波动率下降。平值Vega最大,深度价外时,Vega值接近于零。
如果某期权Vega为0.15,若价格波动率上升(下降)1%,期权的价值将上升(下降)0.15。若标的价格波动率为20%,当其上升为22%时,波动率变化了1%,其它条件不变的情况下,期权理论价值上升(下降)0.15。
多空调换及无风险套利中的风险对冲
对于由许多行权价组成的做市商类型头寸,如果标的物从多头变动到空头,获益获得最大盈利。随着标的物价格变动及穿多头行权价,可以得到Gamma多头盈利,当标的物达到空头行权价,可以收获Theta盈利。
如果市商卖出一种期权,就需要买入一种不透的期权对冲整体头村风险。很多交易员在持有Gamma或Vega多头时,需要卖出期权,就降低期权的买价和卖价,持有Gamma或Vega空头时,则提高买卖价。
五、Rho
1. Rho值概念
Rho时指期权价格对无风险利率变化的敏感程度。对于一般交易者来说,Rho在实际交易中运用的不多,更多时运用在期权平价理论中。Rho衡量的时利率升跌1%对权利金的影响,时计算利率变动风险的指标。大多数期权定价模型对同一个执行价上的看涨和看跌分别给出Rho值。公式表达为:
\rho=\frac{期权价格变化}{无风险利率的变化}2. Rho值特性
一般来说,期权买方的Rho是正值,卖方的Rho是负值。随着无风险利率的增大,执行价格会下降,期权价值会增加。
当利率上涨时,Call价值上涨与利率上升相同的点数,而Put价值下跌同样的点数。
距离到期日时间越长,期权的Rho就越大,利率对期权的影响越大。
对于欧式期权来讲,期权平价公式的利息是有执行价格计算来的,所以可以认为执行价格越高,利率对价格的影响越大。
实值程度越深,Rho越大,而虚值期权Rho值接近于0。
总结
Delta、Gamma、Theta、Vega、Rho是预测期权权利金变化的工具,涉及决定权利金的四项因素:标的物价格、时间流逝、波动率、利率。
风险分析非常重要,对风险性质和交易管理不充分很容易遭受损失,但过度忧虑风险,就不能拟定交易决策。
我们可以借助希腊参数来识别风险、指导交易,通过组合头寸的净希腊参数,交易员可以获得一些在Delta、Gamma、Vega、Theta和Rho上的风险敞口信息。
另外,在实际的期权交易中,对于期权头寸组合的风险管理,交易不仅要关心单个头寸的Delta、Gamma、Theta、Vega和Rho,还要关心作为一个整体组合的希腊参数。
对于在实际交易中不断变动部分的大头寸,需要监控和调整每一个部分以确保整体和谐运行,所以保持平衡策略也很重要。