我们在解马赛克算法或者超分辨率算法中常常用边缘方向来指导插值,对demosaicing算法而言,边缘引导插值发生在整像素位置,对super resolution算法而言,边缘指导插值常常发生在亚像素位置。这篇博客简单总结解马赛克中一种常用的插值方法:自适应边缘插值算法。
除了自适应边缘插值,也给了一些常用的其它解马赛克算法的介绍:微软解马赛克算法、基于色差残差的插值算法、经典的GBTF、RI等算法给了链接索引。
demosaicing 算法的插值总是发生在整数位置,在bayer pattern中,我们常常先插值G通道,再插值R通道和B通道。插值R和B通道时,常常使用色差图或者残差图进行插值。
色差法
1)先恢复 G 点的 R 和 B ,可以采用最简单的双线性插值或者其他插值方法。
2)求 G 点的色差:利用 G 减去得到的 G 点的 R 和 B ,得到 G-R,G-B 。其位置分布 与 G 相同。
3)对 G-R 和和 G-B 进行插值,求出 bayer 中原始 R 位置对应的 G-R 和原始 B 对应 的 G-B
4)求 Bayer 中 R 位置的 G 和 B 位置的 G :将原始 R 加上 R 位置的 G-R 就得到 R 位置 的 G ,将原始 B 加上 B 位置的 G-B 就得到 B 位置的 G 。 经以上4步,至此我们得出了一幅完整的G。

计算色差图,定义
Kr=G-R\\ Kb=G-B
以 Kr 举例,对没有R像素数值的像素,需要对Kr附近的像素进行数值统计
Kr_{3,3}=G_{3,3}-R_{3,3}=G_{3,3}-(R_{3,2}+R_{3,4})/2 \\
Kr_{2,4}=G_{2,4}-R_{2,4}=G_{2,4}-(R_{1,4}+R_{3,4})/2插值过程中,先对G通道进行插值,得到所有的G,然后再计算R和B
(1)G通道插值,在计算G值之前,需要先计算好周围的Kr或者Kb,以R点处的G值为例
R_{G_{3,2}}=R_{3,2}+(K_{R_{2,2}}+K_{R_{3,1}}+K_{R_{3,3}}+K_{R_{4,2}})(2) R、B通道插值
以红色为例,有两种情况,分别是G(3,3)处的R值 和 B(2,3)处的R值
R_{G_{3,3}}=R_{3,3}+(K_{R_{1,3}}+K_{R_{3,2}}+K_{R_{3,4}}+K_{R_{4,3}}) \\
R_{B_{2,3}}=G_{B_{2,3}}+(K_{R_{2,3}}+K_{R_{3,2}}+K_{R_{3,4}}+K_{R_{4,3}})自适应边缘插值算法 Hamilton and Adams

我们以绿色像素插值为例
(1)计算水平梯度和垂直梯度,以B(2,3)举例
\nabla H=|G_{2,2}-G_{2,4}|+|2*B_{2,3}-B_{2,1}-B_{2,5}| \\
\nabla V=|G_{1,3}-G_{3,3}|+|2*B_{2,3}-B_{-1,3}-B_{4,3}|(2)分析梯度数值大小,计算插值的G值
这里插值时除了考虑G通道,还考虑了二阶微分,可以利用B通道恢复较强的边缘,这里也隐含了前面说的色差法,利用了通道和通道之间的色差一致假设:
\nabla H < \nabla V: \ \ \ \ G_{B_{2,3}}=(G_{2,2}+G_{2,4})/2+(2*B_{2,3}-B_{2,1}-B_{2,5})/4 \\
\nabla H > \nabla V: \ \ \ \ G_{B_{2,3}}=(G_{1,3}+G_{3,3})/2+(2*B_{2,3}-B_{-1,3}-B_{4,3})/4 \\
\nabla H = \nabla V: \ \ G_{B_{2,3}}=(G_{1,3}+G_{2,2}+G_{3,3}+G_{2,4})/4 + (4*B_{2,3}-B_{-1,3}-B_{4,3}-B_{2,1}-B_{2,5})
(3)插值绿色通道缺失的红、蓝数值
寻找附近一列或者一行存在红色像素进行权重插值
R_{G_{3,3}}=(R_{3,2}+R{3,4})/2+(2*G_{3,3}-G_{3,1}-G_{3,5})/4蓝色插值同上
(4) 插值红(蓝)通道处缺失的蓝(红)像素
还是一B(2,3)举例,定义倾斜梯度:
\nabla N = |R_{1,2}-R_{3,4}|+|2*G_{2,3}-G_{1,2}-G_{3,4}| \\
\nabla P = |R_{1,4}-R_{3,2}|+|2*G_{2,3}-G_{1,4}-G_{3,2}|根据倾斜梯度选择插值方向:
\nabla N < \nabla P: \ \ \ \ G_{B_{2,3}}=(R_{1,2}+R_{3,4})/2+(2*G_{2,3}-G_{1,2}-G_{3,4})/4 \\
\nabla N > \nabla P: \ \ \ \ G_{B_{2,3}}=(R_{1,4}+R_{3,2})/2+(2*G_{2,3}-G_{1,4}-G_{3,2})/4 \\
\nabla N = \nabla P: \ \ G_{B_{2,3}}=(R_{1,2}+R_{3,4}+R_{1,4}+R_{3,2})/4+(4*B_{2,3}-G_{1,2}-G_{3,4}-G_{1,4}-G_{3,2})/4微软解马赛克算法
微软解马赛克算法是Matlab中默认的demosaicing算法,2004年提出,好处是计算简单,几个简单的线性滤波就搞定了
Paper: https://www.microsoft.com/en-us/research/wp-content/upload/2016/02/Demosaicing_ICASSP04.pdf
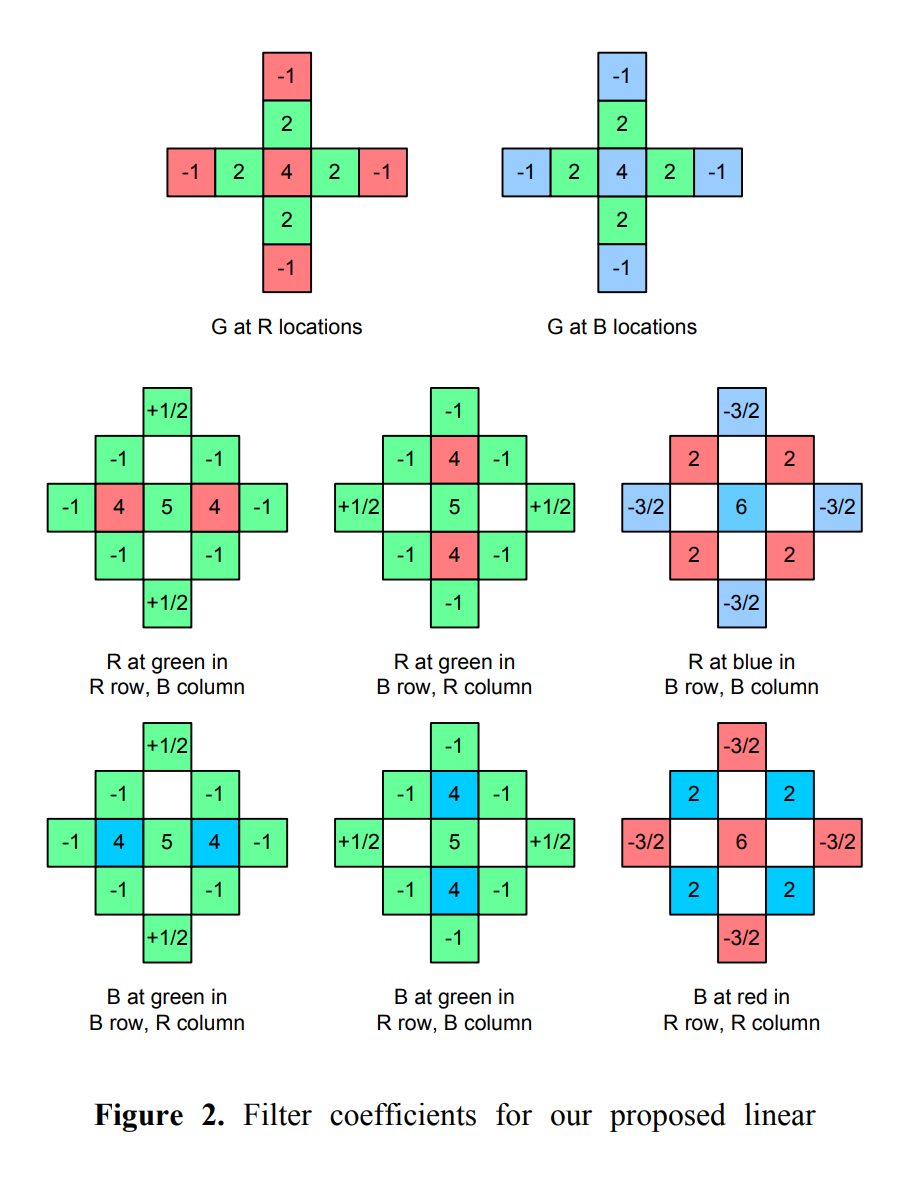
GBTF算法
Gradient based threshold free color filter array interpolation
主要是基于色差来做
IR算法
主要是基于残差图引导滤波来做
有两个比较经典的demosaicing算法,简单贴下paper和图:
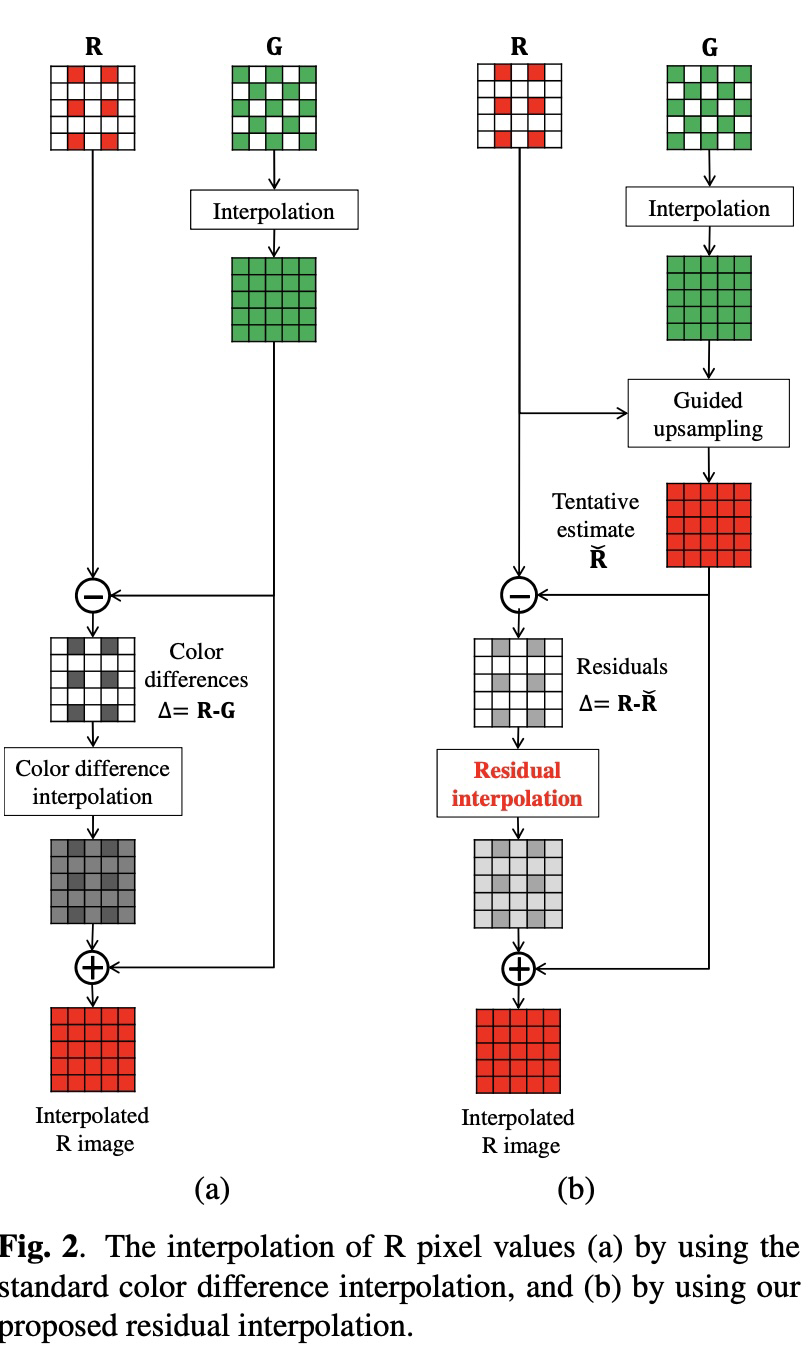
参考书籍
对于去除混叠和False Color,在这本书有介绍:
提供一个下载地址:图像信号处理书籍推荐
