简单记录一下Mamba相关几篇paper的创新和改进过程,首先SSM把RNN和CNN结合起来,可以像RNN一样推理(更快),也可以像CNN一样训练。然而SSM依然无法像Attention一样捕捉长程依赖,于是S4通过改进SSM中的矩阵运算将运算复杂度降低,这样就可以实现一个更大规模的输入。Mamba(S6)进一步解决了输入选择性、并行结算、结构简化的问题。
一、SSM
定义:
- 输入序列x
- 隐藏状态h
- 输出序列y
h'(t)=Ah(t)+Bx(t) \\ y(t)=Ch(t)+Dx(t)
图解计算流程:
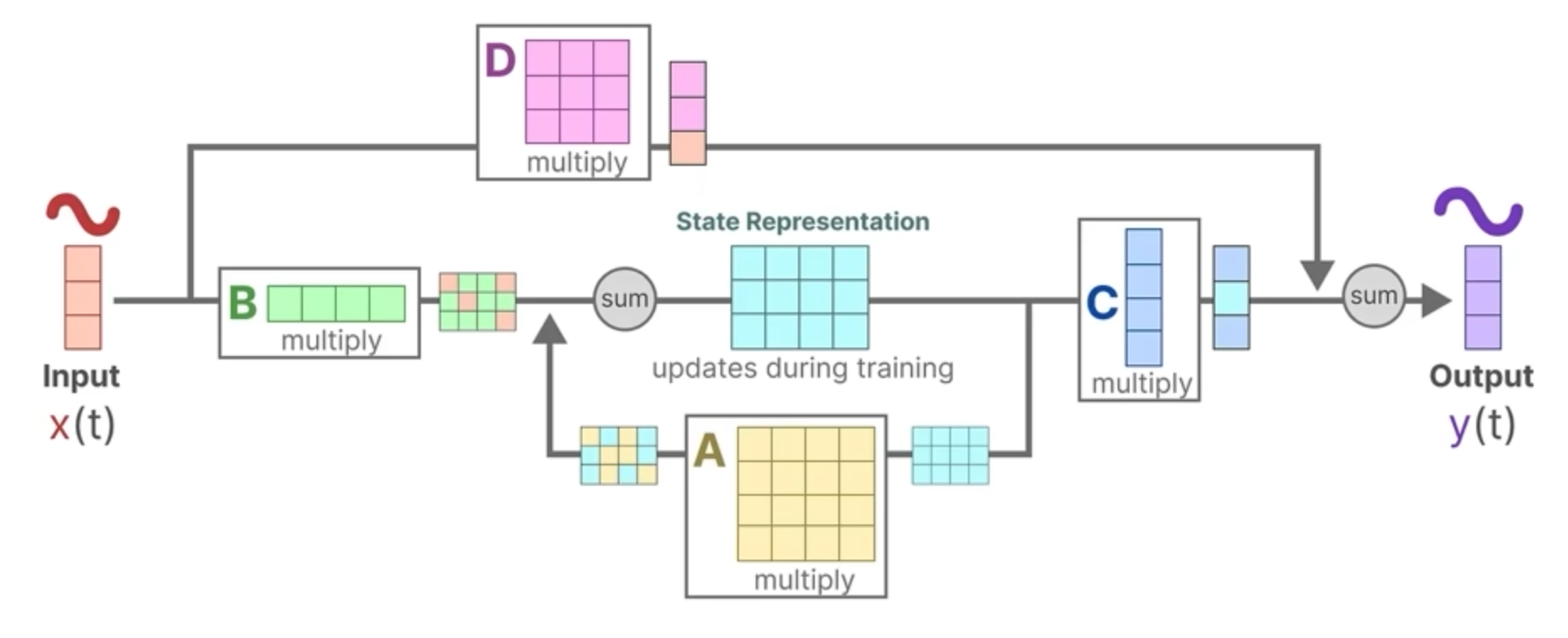
二、S4
Structured State Space for Sequences
SSM和CNN、RNN一样无法有效捕捉长程依赖,解决方法是使用HiPPO矩阵替代A矩阵
矩阵分解:使用两个长度为N的矩阵PQ就可完成A矩阵相关运算,复杂度由O(N^2)降低到O(N)
A=VVV-PQ^T=V(A-(V^*P)(V^*Q)^*)V^*
三、S6(Mamba)
S4与SSM的问题:无选择性。ABC矩阵在训练完成时就会固定,不论输入时什么,都会通过完全一样的A,这样导致ABC无法根据输入做针对性推理。
如果ABC会根据输入变化,那么就无法将SSM转化为标准卷积过程。于是Mamba的motivation就是:
- 参数化矩阵:AB矩阵变为输入数据驱动
- 硬件感知的并行运算算法
- 更简单的SSM结构

先接晒下上面各个数据维度(B,L,N)的含义:
- B: Batch Size
- L:序列长度
- D:每个时间step的序列特征维度
- N:隐状态的维度
不直接把AB参数化成(B,L,D,N)的尺寸,一方面会造成参数量增大,另一方面,通过上下文推导带有delta项的运算,因此只需要参数化成如上的尺寸即可实现AB的参数化。

硬件感知算法:算法并行化(选择性扫面算法)
定义了一种 Add 运算符,假设运算操作顺序与关联矩阵A无关,会发现每个xt乘以的矩阵都源于xt本身(矩阵BC是x通过线性层得到的),该运算满足交换律和结合律,虽然不是卷积但也是一种并行运算。

举个例子,对于y3
y_3=C\bar{A_3}\bar{A_2}\bar{A_1}\bar{B_0}x_0+C\bar{A_3}\bar{A_2}\bar{B_1}x_1+C\bar{A_3}\bar{B_2}x_2+\bar{B_3}x_3
更简单的SSM结构:一路是数据过Conv和SSM Block,另一路充当一个门控,对数据进行筛选
